封闭音响系统构造

本文翻译自 RICHARD H. SMALL的Closed-Box Loudspeaker Systems Part Ⅱ:Synthesis一文
（上文接 RICHARD H. SMALL 的 Closed-Box Loudspeaker Systems Part I: Analysis（封闭音响系统分析））

八、讨论

8.1 驱动单元尺寸

长期以来，人们普遍认为大型低音单元优于小型低音单元。虽然这种观点似乎被经验所证实，但最近有人对此提出了质疑。本文的分析表明，仅靠驱动单元的尺寸，并不能决定或限制系统在小信号响应、效率或位移限制下的功率容量等方面的性能。
在具有相同小信号和大信号参数（本文讨论的类型）的前提下，大型单元的成本不可避免地高于小型单元。然而，从物理角度来看，大单元更容易获得较大的 （即体积位移），从而具有更高的声功率容量；并且，与输出相同声功率的小型单元相比，大型单元产生的调制失真较小。
因此，就小信号响应和效率而言，大单元并不具有固有优势，甚至可能在成本上存在劣势。但如果需要在低失真的情况下输出高声压，则大型驱动单元具有明确优势。

8.2 箱体尺寸

从第四节可以看出，具有高顺从比（compliance ratio）的空气悬挂系统可以复制传统低顺从比的大型密闭箱系统的性能。然而，一旦顺从比大于约 4，就无法在不影响系统性能的前提下进一步显著减小箱体体积。一个小型的空气悬挂系统，与一个大型的空气悬挂系统相比，必须具有更高的截止频率，或更低的效率，或者两者兼有。
虽然人们多次声称，可以设计一个小系统以拥有与大系统相同的响应，但如果两者都是高效利用的空气悬挂设计，那么如公式（26）或图 8 所示，小系统的效率必然低于大系统，其效率与体积成正比。通常可以让小系统具有与大系统相同的最大声输出和频率响应，但其较低的效率意味着需要更高的输入功率，因此驱动单元的音圈必须具备更强的散热能力。此外，很容易证明，在这种条件下，小系统的驱动单元将需要更大的磁铁（例如：要驱动一个相同尺寸但更重的振膜达到相同位移，或驱动一个相同质量但更小的振膜达到更大位移）。因此，在这种条件下，小系统的驱动单元成本必然高于大系统。
可以得出结论：设计越来越紧凑的高品质扬声器系统的压力，直接导致系统效率降低，并且在大多数情况下，声功率容量也会降低。如果不牺牲声功率容量，那么这些紧凑系统需要昂贵的驱动单元，并且必须配备高功率放大器。

8.3 性能规格

在所有用于音频录制与重放的组件中，扬声器系统的性能规格是最不完整、信息最少的。至少在低频范围内，情况本不该如此。如果向直射式扬声器系统施加一个规定电压，那么其在低频下的输出可以用声体积速度表示，并且这个值几乎不受声负载影响。用这种方式表示的扬声器系统“响应”对大多数用户而言毫无意义，但如果将这种声体积速度对应到标准自由场负载下产生的声功率或远场声压，则既有意义又实用。
虽然扬声器在房间中产生的声压不同于在自由场中产生的声压，但这种差异显然是由房间属性决定的，而非扬声器系统本身。如果房间表现很差，可以通过声学方式或某些情况下使用电子方式进行修正。这绝不是使用标准自由场负载来准确规范扬声器系统基本响应的障碍。
事实上，Allison 与 Berkovitz 的研究表明 [R. F. Allison and R. Berkovitz, “The Sound Field in Home Listening Rooms,” J. Audio Eng. Soc., vol. 20, no. 6, p. 459 (July/Aug. 1972).] ， 球面自由场负载非常接近典型房间负载的近似值。
当然，这种标准负载方法多年来已被用于扬声器测量标准中。若能更广泛地应用，将为扬声器系统提供一种目前尚不存在的非常有用的定量比较方式。该方法在规范系统低频响应时尤其具有吸引力，因为自由场下的标称低频响应与参考效率可以很容易地从系统的基本参数获得。少数制造商已经提供这些基本参数，或直接提供相关的自由场响应与效率数据。这种做法值得推广。

8.4 典型系统性能

1969 年末，对若干英美及欧洲产的密闭箱系统进行了采样测试，方法是测量其小信号参数，然后根据第三和第四节的关系推导其频率响应和效率。
系统共振频率 (f_c ) 范围为 40Hz 到 90Hz。总 Q 值 (Q_TC）范围为 0.4 到 2.0 。参考效率 (η_o) 范围为 0.28% 到 1.0% 。虽然参数组合没有统一规律，但几乎所有系统都可分为两类：

1. 截止频率 (f₃ ) 低于 50Hz，几乎无峰值响应（ Q_TC 最大到 1.1），体积通常大于 40dm³(1.4ft³) ；
2. 截止频率高于 50Hz，明显有峰值响应（ Q_TC 在 1.4 至 2.0 之间），体积小于 60dm³(2ft³) 。

对于这一现象，一位销售这两类美国系统的销售员自发地给出了说明（并做了演示）：
只有第 1 类系统能再现管风琴与交响乐的低频基础，而第 2 类系统在播放流行音乐时有明显更强的低音。因此，销售往往取决于顾客的音乐口味。
这在营销上讲得通，在经济上也说得通，因为在大箱体中表现为第 1 类性能的同一驱动单元，在小箱体中则表现为第 2 类性能——具有更高声功率容量。

九、系统合成

9.1 系统与驱动单元的关系

大多数密闭箱系统使用输出阻抗可忽略不计的放大器，运动质量不超过裸置驱动单元的质量，并且其总阻尼主要来自驱动单元的电磁耦合与机械损耗。
在这些条件下，可由公式（7）、（9）、（13）、（17）与（18）推导出：

\[ \frac{Q_{\text{TCO}}}{Q_{\text{TS}}} = \frac{Q_{\text{EC}}}{Q_{\text{ES}}} = \frac{f_c}{f_s} = (a+1)^{\frac{1}{2}} ······(54) \]

因此，

\[ \frac{f_c}{Q_{\text{TCO}}} \approx \frac{f_s}{Q_{\text{TS}}} ······(55) \]

其中 Q_TS 是驱动单元在频率 f_s 下、源阻抗为零时的总 Q 值，即：

\[ Q_{\text{TS}} = \frac{Q_{\text{ES}} Q_{\text{MS}}}{Q_{\text{ES}} + Q_{\text{MS}}} ······(56) \]

这些公式说明，对于任何特定的箱体-驱动单元组合（即某个特定的 α 值），系统的共振频率与 Q 值与驱动单元的相同比例增长，增长因子为 (a+1)^1/2 。该关系在图 13 中作为函数 α 绘出。

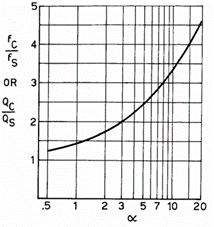
该近似关系，以及前文推导的响应、效率与功率容量的基本关系，将在下文中用于两种重要情况的系统设计程序开发：一种是固定驱动单元设计，另一种是仅给定系统最终性能指标的情况。

9.2 设计已知单元的系统

设计一个与特定单元“匹配”的音箱的一个困难在于，该单元可能从一开始就是完全不适合的。一个用于封闭箱系统单元是否适合的便捷测试由公式 (51) 和 (54) 提供；需要已知或测量单元的参数。公式 (54) 要求单元的谐振频率必须始终低于系统的谐振频率。如果设计者希望避免浪费空间的音箱，即希望设计一个气悬系统，则参数 α 必须至少为 3，且单元的谐振频率必须不超过系统可容忍最大谐振频率的一半。
类似地，Q_TS 必须低于可接受最大值 Q_TCO，且大致与 f_g 与期望或可接受最大值 f_c 的比值相同。最后，根据公式 (51)，V_AS 的值必须至少是期望音箱体积的几倍。
如果单元参数看起来合适，系统设计过程如下：选择满足公式(55)的最佳组合 和 ，然后通过公式(17)计算 。所需的音箱体积（净内部容积）则由公式(51)得出：

\[ V_B = \frac{V_{\text{AS}}}{a} ······(57) \]

若填充吸音材料，该值可以略小。参考效率通过公式(23)计算，声功率额定值由公式(39)或(42)得出。
电功率额定值则由第五节推导得出：

\[ P_{\text{ER}} = \frac{P_{\text{AR}}}{\eta_0} ······(58) \]

9.3 已知单元的设计示例

使用标准挡板和无衬里测试音箱，发现一个欧洲生产的、用于气悬系统的 12 英寸低音单元具有以下小信号参数：

\[ f_g = 19\,\text{Hz}\] \[ \] \[ Q_{\text{MS}} = 3.7\] \[ \] \[ Q_{\text{ES}} = 0.35\] \[ \] \[ V_{\text{AS}} = 540\,\text{dm}^3 \quad (19\,\text{ft}^3) \]

利用公式(56)和(23)可得：

\[ Q_{\text{TS}} = 0.32\] \[ \] \[ \eta_0 = 1.02\% \]

制造商给出的功率额定值为 25W，峰值线性位移估计为 6mm（ 英寸），有效振膜半径估计为 0.12m，因此

\[ S_D = 4.5 \times 10^{-2}\,\text{m}^2, \quad V_D = 2.7 \times 10^{-4}\,\text{m}^3 = 270\,\text{cm}^3 \]

此单元的 f_s 、 Q_TS 和 V_AS 值相当理想。在表 1 中，列出了不同 值下期望得到的 f_c 、 Q_Tco 和 f₃ 对应的音箱体积 V_AB（未填充材料）。

α	fc(Hz)	QTco	f0(Hz)	VAB(dm3)
4	42.5	0.72	42	135
6	50.3	0.85	44	90
9	60.0	1.01	47	60
12	68.6	1.15	50	45

表1 已知单元的期望性能

当 α=4 时，系统响应几乎是 B₂ 型，对应未填充箱体容积为 135dm³（4.8立方英尺），适合落地音箱。
当 α=9 时，仅需 60dm³（2.1立方英尺）即可获得出色表现。
当 α=12 时，可望在 40dm³（1.4立方英尺）填充音箱中实现，此时 Q_Tco 会比表中更低，约为1，对应截止频率约为 53Hz，适合作为“书架式”音箱。
采用体积较大的 对齐系统时，基于公式(42)计算的位移限制声功率为：

\[ P_{\text{AR}} = 0.19\,\text{W} \quad \]

对应电功率为：

\[ P_{\text{ER}} = 19\ \text{W} \]

这低于制造商额定 25W，因此可以安全地配用连续功率为 20W 的功放。
对于“书架式”设计，由于 f₃ 更高，其位移限制声功率约为 0.5W，电功率为 50W，远超制造商额定值。鉴于缺乏制造商额定功率 P_p(max) 的具体依据，建议将功放功率限制在 25W，此时可获得声功率输出为 0.25W。

9.4 根据规格进行设计

大多数工程产品都是为了满足特定的需求而设计的。通常，一个产品的“需求”中包含相互矛盾的因素，工程师需要评估这些需求并对其进行调整，使其在物理和经济上可实现。
例如，图 8 让许多市场经理感到沮丧，他们希望推出一个体积仅为 1 立方英尺（28dm³）的气悬系统，同时能在 20Hz 时保持平坦响应并具有高效率。
一个密闭箱扬声器系统所期望的响应可能基于幅度、相位、延迟或瞬态响应的考虑，但始终可以简化为对 f_c 和 Q_TC 的规范。一旦响应被确定，箱体容积 V_B 或参考效率 η_o 中就可以独立地指定一个；另一个则会被确定或限制在最小或最大值内。最后，功率容量可以以 P_ER 或 P_AR 的形式规定。如果这两个功率都必须独立固定，那么这将决定 η_o ，从而如上所述限制 V_R 。
一个典型的设计规范集可能从 f_c , Q_TC , V_B 和 P_AR 的数值开始，并配以一个固定的额定阻抗，从而确定 R_E。除非使用的是特殊放大器，否则可假设 Q_TC =Q_ToC 。注意， V_B 有效地规定了箱体；设计问题因此变成了指定驱动单元。
设计过程首先是为 Q_MC 和 α 赋予合理的值。 Q_MC 对系统性能的影响仅通过 K_η(Q) 体现，相对较小。如第 7 节所述，使用填充材料的系统通常取值为 2~5，未填充系统为 5~10。如果无法获得更好的估计，可假设 Q_MC=5 。然后使用公式(9)计算系统所需的 Q_EC 。
如果希望在初始规范范围内达到最大效率，则必须使用气悬原理。这要求 α 至少为 3 或 4，但其值对系统性能影响较小，仅通过 K_η(c) 体现，可以选择任何在物理可实现范围内的值。如果选择过大，驱动器将需要不现实地高的顺应性，这即使能实现，也可能导致悬挂系统的机械稳定性差。合适的 α 一般在3~10之间。
接着确定 V_AB 的值。对于未填充系统，V_AB=V_B ；若有填充，则需乘以 1.4/γβ （通常为1.15~1.2）的因子增加。
然后根据公式(17)和(18)计算所需的驱动单元小信号参数：

\[ f_S = \frac{f_C}{\sqrt{a+1}} ······(59) \] \[ \] \[ Q_{\text{ES}} = \frac{Q_{\text{EC}}}{\sqrt{a+1}} ······(60) \]

以及

\[ V_{\text{AS}} = aV_{\text{AB}} ······(51) \]

V_TA 由公式(49)确定。完成的系统预期的参考效率由公式(24)计算。或者，分别评估 K_η(Q) , K_η(G) 和 K_η(G) ，再用公式(26)求出 η₀ 。系统的电功率额定值 P_ER 则由公式(58)计算。根据程序材料的峰值与平均功率比，可分配一个相当或更低的 P_B(MAX) 值。所需的 V_D 值可以直接通过公式(39)计算，结合图 5 或公式(78)确定 |X(jω)|_max；也可以使用公式(42)，按具体情况选用。该值必须不大于 V_B 的几个百分点。
此时，驱动单元已由其最关键参数定义 f_S ,Q_ES ,V_AS ,V_D 和 P_E(max)，再加上音圈电阻 R_E，通常为所需额定阻抗的 80%。系统设计者此时面临的问题是如何获得具有这些参数的驱动单元。如果他有自己的驱动单元工厂，就可以如下一节所述那样定制驱动单元。如果没有这种条件，就必须在市场上寻找符合要求的产品。
目前市面上销售的大多数扬声器单元都未提供完整的参数信息，无论是否采用上述形式。不过，随着对制造商参数透明度的要求日益提高，这一情况将逐步改善。如今的系统设计者应尽可能获取样品并按所述的方法自行测量参数。小信号参数应在标准测试障板上测量，障板面积为 1 或 2 平方米，这样可确保振膜所受的空气负载与在系统箱体中时相近。

9.5 规格设计示例

设计一个密闭式气悬扬声器系统，该系统将与一个高阻尼因子的放大器配合使用，需满足以下规格：

项目	说明
f3	40Hz
响应特性	B2 响应
箱体容积	2ft3(56.6dm3 )
声功率额定值	0.25 W 程序峰值； 预期峰值/平均比为5 dB

箱体将带有内衬但不填充。假设箱体和驱动单元的损耗对应 Q_MC=5，且可以实现的顺应比为 α=5 。
前两个规格直接转换为：

f_c=40Hz

以及

Q_TC=Q_TCO=0.707

对于 Q_MC=5 ，根据公式(9)得：

Q_EC=0.824

对于 α=5，有 (α+1)^1/2=√6=2.45 ；因此根据公式 (59) 和 (60)：

f_s=16.3Hz

和

Q_ES=0.336

另外，对于未填充箱体，根据公式(51)得：

V_AS=10ft³ (283dm³ )

接着，根据公式(49)得：

V_AT =1.67ft³ (47.2dm³ )

根据公式(29)、(30)和(31)，

k_η(Q)=0.858
k_η(G) =0.833
k_η(G) =1.36×10^-6

因此，

k_η=0.97×10^-6

并根据公式 (26)，

η_o=0.00351 或 0.35%

参考效率也可以直接由公式(24)计算，因为 f_C、V_AT 和 Q_EC 是已知的。 根据公式(58)，位移限制的电功率额定值为：

P_ER=71.5W

为了获得指定的声学输出，必须使用这种功率等级的放大器。对于预期的峰值/平均功率比，驱动器的热功率额定值P”E(max)” 至少应为22.5W。
根据公式(42)计算程序功率额定值：

V_D=3.4×10^-4m³ 或 340cm³

这仅是 V_B 的 0.6%，因此空气顺应性的线性度不是问题。

十、驱动器设计

10.1 一般方法

系统设计过程最终要用基本参数来规定所需驱动器的要求。这些参数用于驱动器的物理设计。
首先，必须将 V_D 分解为可接受的 S_D 和 x_max 的数值。S_D 的选择可能需要在成本、失真和可用安装面积之间进行折中。
振膜悬挂系统所需的机械顺应性为：

\[ C_{\text{AS}} =\frac{C_{\text{AS}}}{S_D^2}= \frac{V_{\text{AS}}}{\rho_0 c^2 S_D^2} ······(61) \]

所需的总机械移动质量为：

\[ M_{\text{MS}} = \frac{1}{(2\pi f_g)^2 C_{\text{MS}}} ······(62) \]

此总移动质量包括任何由填充材料增加的质量，以及振膜前后空气负载M_M1和M_MB。后者可参见文献。振膜和音圈组件的机械质量为： M_MD=M_MS-(M_M1+M_MB )········(63)

\[ M_{\text{MD}} = M_{\text{MS}} – (M_{\text{M1}} + M_{\text{MB}}) ······(63) \]

减去任何由填充材料增加的质量。 磁体和音圈必须提供如下电磁阻尼：

\[ \frac{B^2 l^2}{R_E} = \frac{2\pi f_S M_{\text{MS}}}{Q_{\text{ES}}} ······(64) \]

或者对于指定的 R_E 值，所需的 Bl 积为：

\[ Bl = \sqrt{\frac{2\pi f_S R_E M_{\text{MS}}}{Q_{\text{ES}}}} ······(65) \]

这个 Bl 积以及机械顺应性在振膜位移为 ±x_max 时必须保持良好的线性。这实际上意味着音圈在气隙外的超出长度在每一端大约为 x_max 。此外，音圈必须能够在不损坏的情况下散发电功率 P_B(max) 。这个设计问题是驱动器制造商所熟悉的。
参数 Q_MS 通常在系统性能中作用较小，但也不能完全忽略。在实际设计中，Q_MS 的值常受到与高频性能相关的设计决策影响。如果驱动器振膜在高频时需要避免强烈共振模式，那么外缘悬挂通常设计为最小化从音圈向外传播的振动能量的反射。这意味着能量在悬挂中耗散，从而导致较低的 Q_MS。因此，驱动器的预期用途或制造商偏好的结构方法决定了 Q_MS 的大致值。在封闭箱体系统中，Q_MS 值以及箱体和填充材料的损耗决定 Q_MC，进而影响系统的 k_η(Q) 值。

10.2 使用空气悬挂系的驱动器

如前所述，只要空气悬挂系统的顺应比大于约 3或 4，其精确值就不那么重要。这意味着驱动器的顺应性、谐振频率和 Q 的精确值不是关键因素。实际上，最关键的是移动质量 M_MS 和电磁阻尼 B² l²/R_E。这些可以直接通过系统参数计算得出。将公式(16)、(17)、(18) 代入公式(61)、(62)、(64)，或使用(3)、(6)、(8)、(25)，得到：

\[ M_{\text{AS}} = S_D^2 M_{\text{AC}} = \frac{\rho_0 c^2 S_D^2}{4\pi^2 f_C^2 V_{\text{AT}}} ······(66) \]

以及：

\[ \frac{B^2 l^2}{R_E} = \frac{2\pi f_C M_{\text{MS}}}{Q_{\text{EC}}} ······(67) \]

只要机械顺应性足够高以获得近似的顺应比，其精确值并不重要。这是空气悬挂设计原则的一大优势，因为机械顺应性是生产中最难控制的驱动器参数之一。

10.3驱动器设计示例

上一节示例中所需的驱动器具有以下参数规格：

f_g=16.3 Hz
Q_ES=0.336
V_AS=283dm³
V_D=340 cm³
P_E(max) =22.5 W

为了满足 V_D 和 P_E(max) 的要求，驱动器尺寸可能至少需要为 12 英寸。假设 12 英寸驱动器的典型振膜半径为 0.12m，则： S_D=4.5×10^-2 m²
对于所需的位移体积 340cm³，则峰值线性位移应为：

x_max=V_D/S_D=7.5×10^-3m=7.5mm(0.3in)

总“冲程”要求为15mm（0.6英寸），对于一个 12 英寸驱动器是可以实现的。相比之下，相同的位移体积在 10 英寸驱动器中需要 22 mm（0.9英寸）的冲程，而在 15 英寸驱动器中只需 9.6mm（0.38英寸）。

继续设计 12 英寸的驱动器， S_D²=2.0×10^-3 m⁴

由公式(61)和(62)可得所需的机械顺应性和质量为：

C_MS=9.9×10^-4m/N
M_MS=97g

M_MS 是包括空气负载在内的总移动质量。假设前方空气负载等效于无限障板，并且驱动器振膜占据箱体前表面积的三分之一，则音圈和振膜本身的质量为：

M_MD=M_ms-(3.14a³+0.65πρ₀a³ )=87g

磁阻尼必须为（由公式64得）：

\[ \frac{B^2 l^2}{R_E} = 30\,\text{N·s/m} \quad (\text{MKS机械欧姆}) \]

对于一个标称 “8Ω” 阻抗，R_E 通常约为 6.5Ω。所需的 Bl 值为： Bl=14T⋅m
并且该 Bl 值必须在 15mm（0.6英寸）音圈冲程范围内保持良好的线性。此外，音圈必须能够在不受损的情况下持续耗散 22.5W 的额定输入功率。
关于基于系统小信号需求的驱动器合成的更多示例，可见参考文献 [J. R. Ashley, “Efficiency Does Not Depend on Cone Area,” J. Audio Eng. Soc., vol. 19, no. 10, p. 863 (November 1971).]；其中方法与上述相同，但设计过程可由分时数字计算机自动处理。（参考文献中使用的 Thiele 基本效率 [A. N. Thiele, “Loudspeakers Proc. IREE (Australia), vol. 22, no. 8, p. 487 (Aug. 1961). Also, J. Audio Eng. Soc., vol. 19, no. 5, p. 382; no. 6, p. 471 (May, June 1971).] 是基于4π球面自由场负载，其值为本文所用参考效率的一半。）

十一、设计验证

可按照参考文献 [.R. H. Small, “Direct-Radiator Sys tem Analysis,” IEEE Trans. Audio and Electroacoustics, Loudspeaker vol. AU-19, no. 4, p. 269 (Dec. 1971); als] 中的方法，通过测量驱动器参数来验证按上述方法设计的原型驱动器的适用性。对于空气弹簧系统驱动器而言，不必精确满足 f_s、Q_ES 和 V_AS 的指定值。重要的是参数组合 f_s² V_AS 和 f_s/Q_ES 应与所需值匹配，因为它们共同反映了移动质量和电磁耦合的有效性。如果 V_AS 足够大，以在系统中实现满意的 α 值，则驱动器设计是可接受的。
类似地，可通过第六节所述的方法测量完成系统的参数，并将其与初始规范进行比较来验证系统性能。也可以在消声环境中或使用间接方法对系统性能进行测量验证。
(注： Benson 的一篇最新论文中提出了一种改进的Q测量方法 [J. E. Benson, “Theory and Design of Loudspeaker Enclosures Part 3–Introduction Systems,” to Synthesis of Vented A.W.A. Tech. Rev., vol. 14, no. 4, p. 369 (November 1972)]，可以补偿因音圈感抗较大而引入的误差。该补偿方法是将方程(45)中的 f_c以及参考文献[R. H. Small, “Direct-Radiator Sys tem Analysis,” IEEE Trans. Audio and Electroacoustics, Loudspeaker vol. AU-19, no. 4, p. 269 (Dec. 1971); a]中方程(17)的f_s替换为√(f₁ f₂ )。f_c 和 f_s 的实测值不变，其它公式也不受影响。)

十二、结论

本文所提出的定量关系使得通过规范直接综合进行密闭箱系统的低频设计成为可能，并清楚地显示出是否能够物理实现期望的规范。它们对于希望在特定设计约束下获取最佳小信号和大信号性能组合的扬声器系统设计人员来说是非常有用的。
这些关系也对驱动器制造商具有价值，因为它们揭示了现代密闭箱系统设计所需的基本驱动器参数范围，以及为满足小信号和大信号系统要求而必须配置的昂贵磁性材料的程度。
由于一个完整系统的低频性能取决于少量易于测量的系统参数，因此总是可以为标准自由场条件下的小信号低频性能制定明确规范并进行验证。这类信息比起未标明分贝容差和声学环境的频率极限，更具实际参考价值。
作者希望本文（以及未来针对其它类型直辐射系统的论文）中提供的定量关系和物理限制不仅能对系统设计师有帮助，也能最终促进更统一、真实、精确的产品规范的建立。

十三、致谢

本文是关于直辐射电动扬声器系统低频性能的研究项目的部分成果。作者感谢悉尼大学电子工程学院提供研究设施、指导和支持，并感谢澳大利亚联邦教育与科学部提供的财政资助。
特别感谢 J. E. Benson、R. F. Allison 和 R. H. Frater 对早期稿件的审阅与提出的宝贵修改建议。

十四、附录-二阶滤波器函数

14.1 通用表达式

滤波器函数表通常只给出低通原型函数的细节。高通或带通形式可通过适当变换得到。归一化后的原型低通二阶滤波器函数形式为：

\[ G_L(s) = \frac{1}{s^2 T_0^2 + a_1 s T_0 + 1}, ······(68) \]

其中T_0为滤波器的标称时间常数，a_1决定滤波器的特性。相应的高通滤波函数G_H (s)可通过变换

\[ G_H(s T_0) = G_L\left(\frac{1}{s T_0}\right) ······(69) \]

得到：

\[ G_H(s) = \frac{s^2 T_0^2}{s^2 T_0^2 + a_1 s T_0 + 1} ······(70) \]

方程(68)和(70)与密闭箱系统位移和响应函数的方程(20)和(19)形式完全一致，两组方程在以下条件下是等效的：

\[ T_0 = T_C, \quad a_1 = \frac{1}{Q_{\text{TC}}} \]

研究滤波函数在正弦激励下的稳态幅频响应可通过如下幅度平方形式简化：

\[ |G_L(j\omega)|^2 = \frac{1}{\omega^4 T_0^4 + A_1 \omega^2 T_0^2 + 1} ······(72) \] \[ \] \[ |G_H(j\omega)|^2 = \frac{\omega^4 T_0^4}{\omega^4 T_0^4 + A_1 \omega^2 T_0^2 + 1} ······(73) \]

其中

\[ A_1 = a_1^2 – 2 ······(74) \]

14.2 截止频率

高通函数的半功率频率 ω_3=2πf_3 可通过令上述表达式等于 1/2 并求解 ω 得到。归一化后的半功率频率为：

\[ \frac{f_3}{f_C} = \sqrt{\frac{\frac{1}{Q_{\text{TC}}^2} – 2 + \sqrt{\left(\frac{1}{Q_{\text{TC}}^2} – 2\right)^2 + 4}}{2}} ······(75) \]

14.3 最大幅值频率

响应或振膜位移的最大幅值频率通过对表达式关于频率求导并令其为零得到。
若 Q_TC>1/√2，则最大响应的归一化频率为：

\[ \frac{f_{G_{\text{max}}}}{f_C} = \frac{1}{\sqrt{1 – \frac{1}{2 Q_{\text{TC}}^2}}} ······(63) \]

若 Q_TC≤1/√2，则 f_^Gmax /f_C 为无穷大。
振膜最大位移的归一化频率为：

\[ \frac{f_{X_{\text{max}}}}{f_C} = \sqrt{1 – \frac{1}{(2 Q_{\text{TC}}^2)^2}} ······(77) \]

若 Q_TC≤1/√2，则 fX_max/f_C=0。

14.4 最大幅值

将上述频率值代入|G(jω)|²和|X(jω)|²表达式，得到幅值最大值：

\[ |G(j\omega)|_{\text{max}} = |X(j\omega)|_{\text{max}} = \sqrt{\frac{Q_{\text{TC}}^4}{Q_{\text{TC}}^2 – 0.25}} ······(78) \]

对于 Q_TC>1/√2，若不满足此条件，则最大幅度为 1。

14.5 最大幅值

通过调整 Q_TC，可以获得多种系统对齐方式。以下是一些具有代表性的对齐方式及其简要特性：
巴特沃斯 (Butterworth)最大平坦幅度响应（B2）具有最大幅度平坦性：

Q_TC=1/√2=0.707, f₃/f_c=1.000

贝塞尔 (Bessel)最大平坦延迟响应（BL2）具有最大延迟平坦性：

Q_TC=1/√3=0.577, f₃/f_C=1.272

临界阻尼（Critically-damped）响应是无振铃的最速响应形式：

Q_TC=0.500, f₃/f_c=1.554

切比雪夫 (Chebyshev) 等波纹响应（C2）（当 Q_TC>1/√2 时满足条件，其其他特性由公式（75）至（78）给出）中较为常见的一种配置为：

Q_TC=1.000, f₃/f_C=0.786
|G(jω)|_max=|X(jω)|_max=1.155 或 1.25 dB

上一篇