声学参数在多孔材料耗散模型中的应用与比较
用于预测流体相行为的模型中所使用的“声学”参数数量可以在 1 到 8 之间变化(对于各向同性材料而言)。其中三个参数:静态空气流阻、开放孔隙率和动态扭曲的高频限制,可以直接测量,而通过表征技术可以估计其他参数。
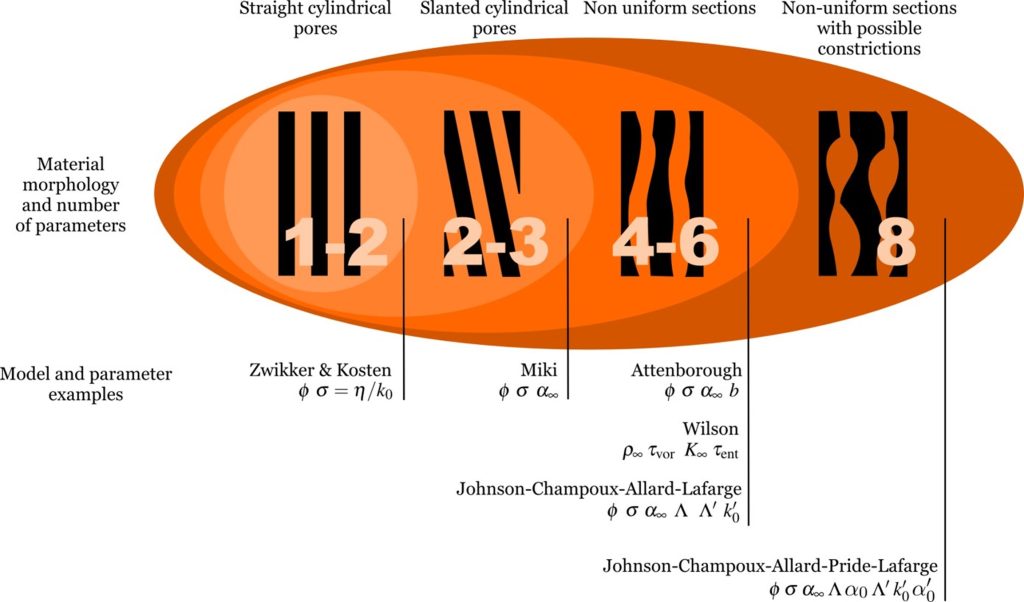
下面报告的表格展示了大量模型所需的参数,用于描述声波在多孔介质中传播时的粘弹热耗散效应。
- Delany-Bazley [DB70] 1-parameter empirical model
- Delany-Bazley-Miki [DB70 Mik90a] 1-parameter empirical model
- Horosehnkov et al. [HGD16,HHG19] a 3-parameter model
- Wilson [Wil93] 4-parameter semi-phenomenologic model
- Johnson-Champoux-Allard [JKD87,CA91] 5-parameter semi-phenomenologic model
- Johnson-Champoux-Allard-Lafarge [JKD87, CA91, LLAT97] 6-parameter semi-phenomenologic model
- Johnson-Champoux-Allard-Pride-Lafarge [JKD87, CA91, LLAT97] 8-parameter semi-phenomenologic model
Delany-Bazley model:
这个基于纤维材料测量结果的经验模型在使用时,应当结合 Miki 提出的修正进行,具体请参阅下文的 Delany-Bazley-Miki 模型。
| 参数 | 表示符号 |
| 静态空气流阻 | σ |
Delany-Bazley-Miki model:
这个经验模型可以用来描述纤维材料的行为。
| 参数 | 表示符号 |
| 静态空气流阻 | σ |
Miki model:
在他发布对 Delany-Bazley 表达式的修正(1990年)的同一年,Miki 还提出了一个包含 3 个参数的模型。
| 参数 | 表示符号 |
| 静态空气流阻 | σ |
| 开放孔隙率 | ϕ |
| 扭曲度的高频限制 | α∞ |
Johnson-Champoux-Allard:
这个半现象学模型可以用来描述纤维材料或具有任意孔形的材料的耗散行为,而不涉及重要的孔截面变化。
| 参数 | 表示符号 |
| 静态空气流阻 | σ |
| 开放孔隙率 | ϕ |
| 扭曲度的高频限制 | α∞ |
| 粘滞特征长度 | Λ |
| 热特征长度 | Λ‘ |
Johnson-Champoux-Allard-Lafarge:
这个半现象学模型可以用来描述具有任意孔形的材料的耗散行为,而不涉及重要的孔截面变化。
| 参数 | 表示符号 |
| 静态空气流阻 | σ |
| 开放孔隙率 | ϕ |
| 扭曲度的高频限制 | α∞ |
| 粘滞特征长度 | Λ |
| 热特征长度 | Λ’ |
| 静态热透过率 | k’0 |
Johnson-Champoux-Allard-Pride-Lafarge:
这个半现象学模型可以用来描述具有任意孔形和重要孔截面变化的材料的耗散行为。
| 参数 | 表示符号 |
| 静态空气流阻 | σ |
| 开放孔隙率 | ϕ |
| 扭曲度的高频限制 | α∞ |
| 粘滞特征长度 | Λ |
| 热特征长度 | Λ’ |
| 静态热透过率 | k’0 |
| 静态黏性扭曲度 | α0 |
| 静态热扭曲度 | α’0 |
Wilson model:
这个半现象学模型可用于描述纤维材料或具有任意孔形的材料的耗散行为,而不涉及重要的孔截面变化。
| 参数 | 表示符号 |
| 动态密度的高频限制 | ρ∞ |
| 涡度模式弛豫时间 | τvor |
| 体模量的高频限制 | K∞ |
| 熵模式弛豫时间 | τent |
References:
The references used in this page are reported hereafter.
[ZK49] Zwikker C. and Kosten C. W., Sound absorbing materials, Elsevier, New-York, 1949.
[Att83] Attenborough K. Acoustical characteristics of rigid fibrous absorbents and granular materials, J. Acoust. Soc. Am. 73(3), pp.785–799, 1983.
[Sti91] Stinson M. R., The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape, J. Acoust. Soc. Am. 89(2), 1991, pp. 550-558 .
[DB70] Delany M. E. and Bazley E. N., Acoustical properties of fibrous absorbent materials, Applied Acoustics 3, 1970, pp. 105-116.
[Mik90a] Miki Y., Acoustical properties of porous materials – Modifications of Delany-Bazley models, J. Acoust. Soc. Jpn (E). 11(1), 1990, pp. 19-24.
[Mik90b] Miki Y., Acoustical properties of porous materials – Generalizations of empirical models, J. Acoust. Soc. Jpn (E). 11(1), 1990, pp. 25-28.
[HGD16] K. V. Horoshenkov, J.-P. Groby, O. Dazel,Asymptotic limits of some models for sound propagation in porous media and the assignment of the pore characteristic lengths, J. Acoust. Soc. Am. 139 (5), 2016, pp. 2463–2474.
[HHG19] K. V. Horoshenkov, A. Hurrell, J.-P. Groby, A three-parameter analytical model for the acoustical properties of porous media J. Acoust. Soc. Am. 145 (4), 2019, pp. 2512–2517.
[Wil93] Wilson D. K., Relaxation-matched modeling of propagation through porous media, including fractal pore structure, J. Acoust. Soc. Am. 94(2), 1993, pp. 1136-1145.
[JKD87] Johnson D. L., Koplik J. and Dashen R., Theory of dynamic permeability and tortuosity in fluid-saturated porous media, J. Fluid Mech. 176, 1987, pp. 379-402.
[CA91] Champoux Y. and Allard J.-F., Dynamic tortuosity and bulk modulus in air-saturated porous media, J. Appl. Phys. 70, 1991, pp. 1975-1979.
[LLAT97] Lafarge D., Lemarinier P., Allard J.-F. and Tarnow V., Dynamic compressibility of air in porous structures at audible frequencies, J. Acoust. Soc. Am. 102(4), 1997, pp. 1995-2006.
