球面波算子及其平移公式推导全解析：从理论发展到电声学与声场重建应用

球面波算子及其平移公式 的研究始于20世纪中期，最早由 Friedman 和 Russek 在 1954 年提出标量球面波的平移公式，主要用于解决多球体散射问题。此后，Stein 在 1961 年和 Cruzan 在 1962 年将这一理论扩展到矢量波，并引入了微分算子表示法，从而简化了公式的推导过程。这些研究在电声学领域具有重要意义，尤其是在多球体散射问题中，球面波算子能够有效分析声波在多个散射体之间的相互作用，为复杂声学环境中的波传播提供了理论支持。此外，在声场重建方面，平移公式通过将声源的场分布展开为不同位置的球面波，为声场的重建与预测提供了高效的工具，这种方法不仅降低了计算复杂度，还显著提高了声场预测的精度，为声学研究和工程应用提供了重要的技术支持。

接下来，我们将详细分析并验证球面波算子及其平移公式。

首先考虑标量亥姆霍兹方程，如下式(1)所示。

\[ \nabla^2 u + k^2 u = 0· · · · · ·(1) \]

在球坐标系中采用分离变量法可以将解写为式(2)形式。

\[ u_{nm}^{(1)}(r) = j_n(kr) Y_{nm}(\hat{r}) · · · · · ·(2) \]

其中，j_n (kr) 是第 𝑛 阶球贝塞尔函数，描述了径向部分；Y_nm (r ̂) 是标准的球谐函数，表示角向部分，如图1所示；上标(1)通常表示正则（驻）波解。这种分离变量法构造的解满足给定的边界条件，并且利用球谐函数完备正交的性质，可以构成任意解的基底。

平面波 e^ikr 可以展开为球面波的叠加形式，标准展开式如式(3)所述。

\[e^{ikr} = 4\pi \sum_{n=0}^{\infty} i^n j_n(kr) \sum_{m=-n}^{n} Y_{nm}(\hat{r}) Y_{nm}^*(\hat{k})· · · · · ·(3) \]

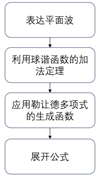
这个公式的推导通常利用下列事实：

1. 球谐函数加法定理与正交性: 利用球谐函数满足的加法定理以及正交关系，可以证明任一函数在球面上可用 Y_nm 展开，并利用生成函数方法（如用 Legendre 多项式的生成函数）得到展开系数。
2. 展开证明思路:从平面波 e^ikr=e^ikrcosγ (其中 cosγ=k ̂·r ̂ )出发，将其写作一个幂级数，并比较两边的球谐函数展开，最后获得上述展开式。这种展开对于任何入射场与散射场之间的转换都十分重要，其展开系数正是通过角动量投影获得。

推导流程如图2所示。

接着我们进行标量波的平移公式推导。令原点处的球面波解 u_nm⁽¹⁾ (r) 平移一个向量 ρ 后，记作 u_nm⁽¹⁾ (r-ρ) ，那么目标是将其重新用原点处的基底 {u_νμ⁽¹⁾ (r)} 展开，即有式(4)。

\[ u_{nm}^{(1)}(r-\rho) = \sum_{\nu, \mu} A(\nu\mu|nm;\rho) u_{\nu\mu}^{(1)}(r)· · · · · ·(4) \]

其中，ν,μ：表示输出的角量子数，即平移后球面波函数在原点处展开时的角量子数；n,m：表示输入的角量子数，即原球面波函数的角量子数；ρ：表示平移向量，描述平移操作的几何位置。竖线（|）分隔的两组变量(νμ)和(nm)表示平移操作前后球面波函数的角量子数。分号（;）后的 ρ 表示平移操作的几何位置参数，强调这是一个独立变量，与角量子数无关。
现在，利用平面波展开与微分算子进行推导。引入微分算子 Θ_nm 定义为 Θ_nm j₀(kr)=i^-nj_n (kr)Y_nm (r ̂) 也就是说，这个算子可以“提取”出角动量部分。利用平面波展开公式可写为式(5)。

\[ e^{ik(r-\rho)} = e^{-ik\rho} e^{ikr} = 4\pi \sum_{n,m} i^n j_n(kr) Y_{nm}(\hat{r}) Y_{nm}^*(\hat{k}) e^{ik\rho} · · · · · ·(5) \]

再利用微分算子作用的等效性，可以写出展出系数的表达式。经过一些数学运算（包括对 e^-ikρ 的球面波展开以及利用正交归一条件），得到式(6)。

\[A(\nu\mu|nm;\rho) = (-1)^\mu \frac{4\pi}{i^{\nu-n}} \Theta_{\nu,-\mu} \Theta_{nm} j_0(k\rho) · · · · · ·(6) \]

这里注意到：指数因子 i^ν-n 出自相应的相位因子匹配；两个微分算子的组合作用于零阶球贝塞尔函数 j₀(kρ) ，从而产生了平移过程中的相应耦合。 对于行波解，也即用第一类球汉克尔函数h_n⁽¹⁾(kr)表示的解，情形与上面类似。定义行波解如式(7)。

\[u_{nm}^{(3)}(r) = h_n^{(1)}(kr) Y_{nm}(\hat{r})· · · · · ·(7) \]

根据区域的不同，我们有：

1.内区 r<ρ: 利用格林函数展开法，可以证明平移后的行波解在内区可以写为式(8)。

\[ u_{nm}^{(3)}(r-\rho) = \sum_{\nu, \mu} A_i(\nu\mu|nm;\rho) u_{\nu\mu}^{(1)}(r)· · · · · ·(8) \]

其中，

\[A_i(\nu\mu|nm;\rho) = (-1)^\mu \frac{4\pi}{i^{\nu-n}} \Theta_{\nu,-\mu} \Theta_{nm} j_\alpha(k\rho) 。 \]

2.外区 r<ρ: 同样通过标量格林函数展开，平移系数为式(9)。

\[A_e(\nu\mu|nm;\rho) = (-1)^\mu \frac{4\pi}{i^{\nu-n}} \Theta_{\nu,-\mu} \Theta_{nm} h_0^{(1)}(k\rho) · · · · · ·(9) \]

这两种情形（如图3所示）均可从平面波展开和微分算子方法出发推导得到，反映了球谐展开在不同区域内的适用性。

最后，我们来求解平移系数。以内区行波展开为例平移系数 A_i(νμ│nm;ρ) 可以展开为式(10)。

\[A_i(\nu\mu|nm;\rho) = (-1)^\mu \sum_{\substack{\alpha=0 \\ \beta=-\alpha}}^\infty i^{n-\nu+\alpha} a(\alpha\beta|\nu\mu nm) j_\alpha(k\rho) Y_{\alpha\beta}^*(\hat{\rho})· · · · · ·(10) \]

其中，α(αβ|νμnm) 是由三重球谐积分给出的耦合因子，其表达为式(11)。这个因子负责将中间耦合过程中的归一化和相位因子引入; i^n-ν+α 是相位因子，来自于平面波展开时 i^l 因子与微分算子激发出相应角动量时的相位调节。

\[a(\alpha\beta|\nu\mu nm) = \sqrt{\frac{(2\alpha+1)(2\nu+1)(2n+1)}{4\pi}} \begin{pmatrix} \alpha & \nu &n\\ 0 & 0& 0 \end{pmatrix} \begin{pmatrix} \alpha & \nu&n \\ \beta & \mu&m \end{pmatrix} · · · · · ·(11) \]

球面波算子及其平移公式作为一种高效的数学工具，近年来在声学领域展现出巨大的应用潜力。通过将复杂的声场分布分解为球面波的叠加，这些公式能够显著简化计算过程，同时提升声场预测的精度和效率。其核心思想在于利用球面波的数学特性，将声学问题转化为更易处理的数学表达形式，从而为解决复杂声学环境中的难题提供了全新的理论支持。在实际应用中，这一工具展现了广泛的应用价值：在建筑声学设计中，它能够优化室内声学性能，帮助设计人员精确预测声波的传播路径和反射特性；在噪声控制领域，它能够精确预测噪声的传播规律，为城市规划和工业噪声治理提供科学依据；在医疗超声成像和声学传感器设计中，它也为高精度成像和传感器优化提供了强有力的技术支持。随着计算技术的不断进步，球面波算子及其平移公式的潜力将进一步释放，不仅能够处理更复杂的声学问题，还将在声学研究和工程应用中发挥更大的作用。未来，随着算法优化和硬件性能的提升，这一工具有望在声学领域实现更广泛的突破，为解决复杂声学问题提供更高效的理论支持和技术创新。