封闭音响系统分析

本文翻译自 RICHARD H. SMALL的Vented-box Loudspeaker Systems Part Ⅳ：Appendices一文

一、背景故事

封闭箱体扬声器系统的理论原型起源于将扬声器安装于足够大箱体以充当无限障板的设计思路。此类系统曾在20世纪中叶以前被广泛采用，凭借大体积箱体来降低低频失真，不过其庞大的体积却不适宜家庭环境使用。
1944 年，Harry F. Olson 与 John Preston 在美国专利申请中提出现代空气悬架扬声器系统的概念，宣告了这一技术的诞生。然而，直至 20 世纪 50 年代，随着高保真声音再现的兴起，该概念才真正走进实际应用领域。1954 年，Edgar Villchur 描述了一种专为高保真再现而设计的紧凑型空气悬架扬声器系统，并与 Henry Kloss 联手创立 Acoustic Research 公司，对这一设计进行商业化推广。这种设计将扬声器置于密封箱体之中，巧妙地借助箱体内空气的弹性来取代传统机械弹簧，从而显著降低了低频失真。
尽管空气悬架扬声器系统在性能上实现了显著进步，但围绕箱体内部填充材料的目的与效果，却引发了一场激烈的公开争议。部分制造商对填充材料的有效性提出质疑，甚至拒绝支付专利使用费，导致 Acoustic Research 公司失去了该技术的专利权。然而，空气悬架方法的基本有效性终究还是凭借其在高保真音响领域的广泛应用，得到了有力的证明。

二、基础分析

闭箱式系统的阻抗型声学类似物是众所周知的，如图1所示。在该电路中，符号定义如下：B 是扬声器气隙中的磁通量密度;l是音圈导体在气隙磁场中的长度；e_g 是电源的开路输出电压；R_g 电源的输出电阻；R_E 是扬声器音圈的直流电阻；S_D 是隔膜的有效投影表面积；R_AS 是扬声器悬架损失的声学阻力；M_Ac 是扬声器振膜组件在音圈和空气负载中的声质量。C_AS 是扬声器悬架的声学顺应性，R_AB 是内部能量吸收引起的外壳损耗的声学阻力；C_AB 是箱体内空气的声学顺应性；U_o 是系统的输出体积速度。
通过将相同类型的串联元件合并，该电路可简化为图2所示的形式。系统的总声顺应性 C_AT 表达式为：

\[ C_{\text{AT}} = \frac{C_{\text{AB}} \cdot C_{\text{AS}}}{C_{\text{AB}} + C_{\text{AS}}}……(1) \]

系统的总阻尼阻抗（总声学电阻）R_ATC 表达式为：

\[ R_{\text{ATC}} = R_{\text{AB}} + R_{\text{AS}} + \frac{B^2 l^2}{(R_g + R_E) S_D^2}……(2) \]

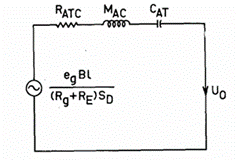
闭箱系统的电气等效电路是通过对图1中的声学电路进行对偶变换，并将其中的每个元件转换为其电气等效形式而得到的。通过将同类元件合并，可以简化该电路，得到图3所示的简化电气等效电路。该电路的布置方式使得实际的音圈端子可以直接接入。

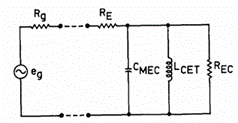
在图3中，符号的定义如下：

\[ C_{\text{MEC}} = \frac{M_{\text{AC}} \cdot S_D^2}{B^2 l^2}……(3) \] \[ \] \[ L_{\text{CET}} = \frac{C_A I^2 B^2 l^2}{S_D^2}……(4) \] \[ \] \[ R_{\text{EC}} = \frac{B^2 l^2}{(R_{\text{AB}} + R_{\text{AS}}) S_D^2}……(5) \]

上述电路仅在驱动单元作为活塞运动的频率范围内有效；在该频率范围内，电路元件被认为是频率无关的。为简化分析过程，忽略了音圈电感和辐射负载电阻的影响。为简化系统分析及其描述函数的理解，定义了以下系统参数。
ω_C (=2πf_C ) 是系统的谐振角频率，定义如下：

\[ \frac{1}{\omega_C^2} = T_C^2 = C_{\text{AT}} M_{\text{AC}} = C_{\text{MEC}} L_{\text{CET}} ······(6) \]

Q_MC 在谐振频率 f_C 下，仅考虑非电阻损耗时系统的品质因数，定义为：

\[ Q_{\text{MC}} = \omega_C C_{\text{MEC}} R_{\text{EC}} ······(7) \]

Q_BC 在谐振频率 f_C 下，仅考虑电阻 $R_E$ 时系统的品质因数，定义为：

\[ Q_{\text{EC}} = \omega_C C_{\text{MEC}} R_{\text{E}} ······(8) \]

Q_TCO 在源电阻 R_g=0 驱动条件下，系统在 f_C 处的总品质因数，定义为：

\[ Q_{\text{TCO}} = \frac{Q_{\text{EC}} Q_{\text{MC}}}{Q_{\text{EC}} + Q_{\text{MC}}} ······(9) \]

Q_TC 考虑系统中所有阻尼因素后，系统在 f_C 处的总品质因数，定义为：

\[ Q_{\text{TC}} = \frac{1}{\omega_C C_{\text{AT}} R_{\text{ATO}}} ······(10) \]

a 是系统顺应比（顺从度比），定义为：

\[ a = \frac{C_{\text{AS}}}{C_{\text{AB}}} ······(11) \]

如果将系统驱动单元安装在一个提供与系统音箱相同空气负载质量的障板上，则根据文献中的公式 (12)、(13) 和 (14)，驱动单元参数变为：

\[ T_S^2 = \frac{1}{\omega_S^2} = C_{\text{AS}} M_{\text{AC}}……(12) \] \[ \] \[ Q_{\text{MS}} = \omega_S C_{\text{MEC}} R_{\text{ES}}……(13) \] \[ \] \[ Q_{\text{ES}} = \omega_S C_{\text{MEC}} R_E ……(14) \]

其中， R_ES=B² l²/S_D² R_ΔS 是表示驱动单元悬挂系统损耗的电阻。驱动单元顺应性等效体积不受空气负载质量影响，其在任意情况下均为：

\[ V_{\text{AS}} = \rho_o c^2 C_{\text{AS}}……(15) \]

其中ρ₀ 为空气密度 (1.18kg/m³)， 为空气中的声速（345m/s ）。
在本文中，除非另有说明，通用的驱动单元参数 f_s（或 T_s ）、Q_MS 和 Q_ES 均默认采用上述数值。
通过比较公式 (1)、(6)、(8)、(11)、(12) 和 (14)，可以看出系统参数与驱动单元参数之间具有以下重要关系：

\[ \frac{C_{\text{AS}}}{C_{\text{AT}}} = a + 1 ……(16) \] \[ \] \[ \frac{f_C}{f_S} = \frac{T_S}{T_C} = \sqrt{a + 1} ……(17) \] \[ \] \[ \frac{Q_{\text{EC}}}{Q_{\text{ES}}} = \sqrt{a + 1} ……(18) \]

对图2和图3所示电路进行分析，并代入上述定义的参数，可以得到系统的响应函数为：

\[ G(s) = \frac{s^2 T_C^2}{s^2 T_0^2 + \frac{s T_c}{Q_{\text{TC}}} + 1} ……(19) \]

振膜位移函数为：

\[ X(s) = \frac{1}{s^2 T_c^2 + \frac{s T_c}{Q_{\text{TC}}} + 1} ……(20) \]

位移常数为：

\[ k_x = \frac{1}{a + 1} ……(21) \]

音圈阻抗函数为：

\[ Z_{\text{VC}}(s) = R_R + R_{\text{EC}} \cdot \frac{\frac{s T_c}{Q_{\text{MC}}}}{s^2 T_c^2 + \frac{s T_c}{Q_{\text{MC}}} + 1} ……(22) \]

其中 s=σ+jω 为复频率变量。

三、相应

3.1 频率响应

闭箱系统的响应函数由式 (19) 给出。它是一个二阶（12 dB/ 倍频程截止）的高通滤波器函数；它包含了闭箱系统的低频幅度、相位、延迟和瞬态响应特性的信息。由于系统为最小相位，这些特性彼此相关：调整一项会决定其他特性的变化。在音响系统中，稳态幅度-频率响应——或简称频率响应——的平坦度与范围通常被认为最为重要。
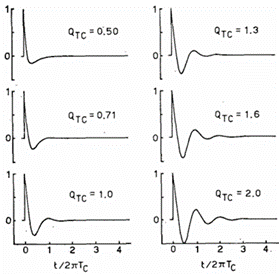
闭箱系统的频率响应 |G(Jω)| 在附录中进行了分析。图4 展示了几个典型的响应曲线，频率轴已归一化为 ω₀ 。对于 Q_TC=0.50 的曲线，是一个二阶临界阻尼对齐；对于 Q_TC=0.71（即 ），是一个二阶巴特沃斯（B₂ ）最大平坦对齐。较高的 Q_TC 值会导致响应中出现峰值，同时带宽相对延伸，初始时带宽的扩展大于相对响应峰值。然而，对于较大的 Q_TC 值，响应峰值继续增加，而带宽的扩展没有显著变化。技术上，对于 Q_TC 大于 1/√2 的响应，是二阶切比雪夫（C2）等波纹对齐。

无论考虑哪种最优响应形状，图4都指示了实现此对齐所需的 Q_TC 值，以及如果 Q_TC 从所需值发生变化（即失配）时响应形状的变化。对于图4中未包含的中间值的 Q_TC ，图5给出了归一化的响应峰值幅度 |G(jω)|_max ，该峰值发生的归一化频率 ，以及响应为 3 dB 低于通带水平时的归一化截止（半功率）频率f_3 / f_C 。

3.2 瞬态响应

闭箱系统对阶跃输入的响应如图6所示，对于不同的 Q_TC 值进行了绘制；时间尺度已归一化为系统共振频率的周期时间。当 Q_TC 值大于 0.50 时，响应呈现振荡特性，且随着 Q_TC 值的增大，响应的幅度和衰减时间也随之增大。

四、效率

4.1 参考效率

密闭箱系统在通带区域的效率，或称系统参考效率，是指在特定空气负载质量下，驱动单元在系统外壳提供的条件下的参考效率。根据文献，参考效率为：

\[ \eta_o = \frac{4\pi^2}{c^3} \cdot \frac{f_s^3 V_{\text{AS}}}{Q_{\text{ES}}} ……(23) \]

其中 f_s,Q_ES 和 V_AS 的值见公式 (12)、(14)和(15)。该表达式可以通过使用第2节中定义的系统参数重写。利用公式(16)、(17)和(18)，可以得到：

\[ \eta_o = \frac{4\pi^2}{c^3} \cdot \frac{f_c^3 V_{\text{AT}}}{Q_{\text{EC}}} ……(24) \]

其中

\[ V_{\text{AT}} = \rho_o c^2 C_{\text{AT}} ……(25) \]

是具有与驱动单元悬挂件和外壳组合的总声学顺应性相同的空气体积。对于 SI 单位，4Π²/C³ 的值为 。

4.2 效率因子

方程(24)可写为：

\[ \eta_0 = k_\eta f_3^3 V_B ……(26) \]

其中
f₃ 是系统的截止（半功率或 -3 dB）频率，
V_B 是系统外壳的净内部体积，
k_η 是由以下公式给出的效率常数：

\[ k_\eta = \frac{4\pi^2}{c^3} \cdot \frac{f_C^3}{f_3^3} \cdot \frac{V_{\text{AT}}}{V_B} \cdot \frac{1}{Q_{\text{EC}}} ……(27) \]

效率常数 k_η 可以分解为三个因子：k_{n(q)} 与系统损耗相关，k_R(O) 与系统顺应性相关，k_η(G) 与系统响应相关。因此：

\[ k_\eta = k_{\eta(Q)} k_{n(C)} k_{n(G)} ……(28) \]

其中：

\[ k_{\eta(Q)} = \frac{Q_{\text{TC}}}{Q_{\text{EC}}} ……(29) \] \[ \] \[ k_{n(C)} = \frac{V_{\text{AT}}}{V_B} ……(30) \] \[ \] \[ k_{n(G)} = \frac{4\pi^2}{c^3} \cdot \frac{1}{\left( \frac{f_3}{f_C} \right)^3 Q_{\text{TC}}} ……(31) \]

4.3 损耗因子

现代放大器的设计目标是具有非常低的输出端口（即西门子阻抗），因此对于实际应用，R_g=0 。任何与这种放大器配合使用的系统的 值等于公式 (9) 给出的Q_TCO 。此时，方程(29)简化为：

\[ k_{n(Q)} = \frac{Q_{\text{TCO}}}{Q_{\text{EC}}} = 1 – \frac{Q_{\text{TCO}}}{Q_{\text{MC}}} ……(32) \]

该表达式的极限值为1，但只有当系统的机械损耗可以忽略时（即 Q_MC 为无限大），所有所需的阻尼才由电磁耦合提供（ Q_EC=Q_TCO ）。
典型的密闭箱系统中，k_η(Q) 的值通常在 0.5 到 0.9 之间。低值通常是故意使用机械或声学耗散来确保较高频率下振膜或悬挂件的充分阻尼，或是为了节省磁性材料和成本。

4.4 顺应因子

方程 (30) 可以扩展为：

\[ k_{\eta(C)} = \frac{C_{\text{AT}}}{C_{\text{AB}}} \cdot \frac{V_{\text{AB}}}{V_B} ……(33) \]

其中

\[ V_{\text{AB}} = \rho_o c^2 C_{\text{AB}} ……(34) \]

是具有与 C_AB 相等的声学顺应性的空气体积。
V_B 是外壳的净内部体积，而 V_AB 是表示外壳声学顺应性的空气体积。若外壳仅包含空气且处于绝热条件下（即没有衬里或填充材料），则V_AB 等于 $V_B$。但是，如果外壳内包含此类材料，则 V_AB 会大于 V_B 。 V_AB 的增加与 γ 的变化成反比，γ 是外壳内空气的比热比，即定压比定容的比值。对于空的外壳， γ 的值为 1.4，当外壳充满低密度高比热材料时， γ 值会减小，接近于 1。方程 (33) 可以简化为：

\[ k_{n(C)} = \frac{a}{a + 1} \cdot \frac{1.4}{\gamma_B} ……(35) \]

其中 γ_B 是适用于外壳的 γ 值。
对于“空”箱体，当 a>>1 时，公式 (35) 有一个极限值为1。空气悬挂系统通常具有介于 3 到 10 之间的 a 值。
如果箱体内填充了材料，1.4/γ_B 项会超过 1，但会产生两个相互作用。首先，由于填充材料增加了 C_AB 的值，因此 a 的值会比空箱体时更低。其次，添加材料会增加箱体内部的能量吸收，从而降低 Q_MC ，并因此减少公式 (32) 中 k_η(Q) 的值。
通过恰当选择填充材料的种类、数量和放置位置， k_η(Q) 与 k_η(C) 的乘积在填充情况下通常比空箱体时略有提高，但提高幅度很少超过约 15%。随意添加未经过选择的材料甚至可能使这两个因子的乘积下降。虽然在理论上可能，但在实际中这个乘积超过1是极其罕见的。有关填充材料的影响将在第7节进一步讨论。

4.5 响应因子

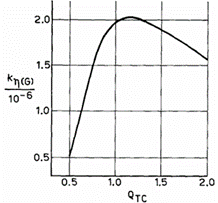
公式(31)中 k_η(G) 的值仅取决于 Q_TC ，因为 (f₃/f_c) 是 Q_TC 的函数，如图 5 和附录中的公式 (75) 所示。图 7 展示了k_η(σ) 随 的变化关系。在 Q_TC =1.1 附近， k_η(G) 达到最大值 2.0×10^-6 。该值对应于一个 C₂ 对齐方式，其通带起伏为 1.9dB。与具有相同带宽的 $B_2$ 对齐方式相比，该对齐方式效率高出 1.8dB。

4.6 最大参考效率、带宽和箱体容积

选择 C₂ 对齐方式下最大效率所对应的 k_η(G) 值，并以 k_η(Q) k_η(G) 的最大可能值为1，理想化封闭箱系统在给定 f₃ 和 V_B 情况下可达到的最大参考效率 ，由公式(26)和(28)得到：

\[ \eta_{o(\max)} = 2.0 \times 10^{-6} f_3^3 V_B ……(36) \]

其中，$f_3$ 的单位为 Hz，$V_B$ 的单位为 m_³ 。图 8 通过将 V_B （以立方分分米表示，1dm³=1升=10^-3m³）与不同 η_o(max) 以百分比表示）对应的 f₃ 关系进行绘图，展示了这一关系。

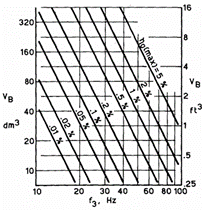
图 8 表示了封闭箱系统设计中效率、带宽与容积之间的物理限制。任何具有给定 f₃ 和 V_B 的系统，其实际参考效率都必须低于图 8 所示的 η_o(max) 。同样，具有指定效率和容积的系统，其截止频率必须高于图8所示值等。这些基本关系在定性上早已为人所知。Finegan 最近也独立给出了这一重要定量限制的表述。
目前有两种方法可以突破由公式(36)或图8所规定的物理限制。一种是“稳定负弹簧原理”，该方法能使 V_ΔT远大于 V_B ，但需要更复杂的设计。另一种方法是使用“功放辅助”，借助均衡网络或专门的反馈技术扩展频率响应 。这种方法需要在扩展响应频段内提供额外的放大功率，同时扬声器单元必须能承受更大的功耗。
任何实际系统的参考效率可直接通过公式 (24) 来评估，只要 f_c、Q_EC 和V_AT 的数值已知或已测量。对于空气悬挂系统，尤其是使用填充材料的系统，V_AT 通常非常接近 V_B 。

4.7 效率-带宽-容积的转换

由公式 (26) 表示的参考效率、带宽和箱体容积之间的关系，以及图 8 中最大效率条件下的图示表明，只要决定 K_n 的因素保持不变，这些系统参数可以相互转换。例如，如果系统变大，可以调整参数以获得更高效率或扩展带宽。同样，如果提高截止频率，也可以调整参数以获得更高效率或更小的箱体体积。如果通过减少机械损耗、添加填充材料、增加 _ 或改变响应形状等方式提高 K_n 的值，则这一提升可体现在更小体积、更高效率、更宽带宽，或这些因素的组合中。每一种选择都要求对箱体或扬声器单元的参数做出特定调整。

五、位移限制的功率额定值

5.1 位移函数

由公式(20)给出的封闭箱体系统的位移函数是一个二阶低通滤波函数。
图9绘制了归一化振膜位移幅值|X(jω)| ，频率相对于 ω_c 归一化，对应多个 Q_TC 值。其曲线与图4中的曲线完全对称。对于中间值的 Q_TC ，图5给出了位移峰值幅度|X(jω)| 和发生该峰值的归一化频率 f_Xmax/f_c 的归一化值。

5.2声学功率额定值

假设大信号振膜位移为线性，封闭箱体扬声器系统的稳态位移限制声学功率额定值 由给出为：

\[ P_{AR} = \frac{4\pi^3 \rho_0}{c} \cdot \frac{f_S^4V_D^2}{ k_x^2 |X(j\omega)|_{\text{max}^2}} ……(37) \]

其中 V_D 为扬声器振膜的峰值位移体积，定义为：

\[ V_D = S_D x_{\max} ……(38) \]

而 x_max 是扬声器振膜的峰值线性位移，通常由音圈的溢出长度决定。将公式(17)和(21)代入公式(37)，则封闭箱体系统的稳态位移限制声功率额定值为：

\[ P_{\text{AR (CB)}} = \frac{4\pi^3 \rho_0}{c} \cdot \frac{f_0^4}{V_D^2 |X(j\omega)|_{\text{max}^2}} ……(39) \]

对于国际单位制，常数 4Π³ρ₀/C 的数值为 0.424。

5.3 功率输出、带宽与位移体积

公式(39)可重写为：

\[ P_{\text{AR(CB)}} = k_P f_3^4 V_D^2 ……(40) \]

其中 $k_P$ 为功率额定常数，定义为：

\[ k_P = \frac{4\pi^3 \rho_0}{c} \cdot \frac{1}{ \left( \frac{f_3}{f_C} \right)^4 |X(j\omega)|_{\text{max}^2}} ……(41) \]

具有特定截止频率 $f_3$ 和扬声器位移体积 $V_D$ 的系统，其声学功率额定值是 k_p 的函数；而 k_p 仅是 Q_TC 的函数，如附录中的(75)和(78)所示。

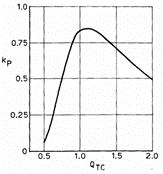
图10绘制了 k_p 随 Q_TC 的变化曲线。最大值出现在 Q_TC 非常接近1.1时。该点对应的几乎就是1.9 dB波动的 $C2$ 对齐状态，也是效率最大的点。在此条件下，公式(40)变为：

\[ P_{\text{AR(CB)}_{max}} =0.85 f_3^4 V_D^2 ……(42) \]

其中 P_AR 以瓦特为单位，f₃ 单位为 Hz， 单位为 m³ 。
公式(42)在图11中展示。$P_{AR}$在左侧刻度以瓦特表示，在右侧刻度表示在 2Π 立体角自由场辐射条件下，一米处的等效声压级（SPL）；该图以 f₃ 为横坐标，针对不同的 V_D 值绘制。右侧刻度所示的一米处 SPL 是一个大致估计，表示平均房间混响场中由左侧给出的声功率产生的声压级。
图11代表了封闭箱体系统设计在大信号下的物理限制。它可用于确定在给定振膜和音圈设计下的最佳性能权衡（ P_AR 与 f₃ 之间），或找出满足特定 f₃ 和 P_AR 规范所需的最小 V_D 值。前文提到的用于克服图8所示小信号限制的技术，并不能改变图11所施加的大信号限制。

5.4 功率输出、带宽和箱体体积

上文给出的由位移限制的功率额定关系并不依赖于箱体体积。在固定响应的条件下，是振膜的位移体积 $V_D$ 控制着系统的功率额定值。然而， V_D 通常不能超过 V_B （箱体体积）的几个百分点；超过这一点，即使驱动单元具有良好的线性，也会由于箱体内空气的非线性压缩而导致不可避免的非线性失真。如果将 V_D 限制为 V_B 的固定比例（该比例取决于可接受的失真程度），则图 11 可重新标注，用以显示在给定失真水平下，为获得特定的 f₃ 和 P_AR 组合所需的最小箱体体积，以及所需的 V_D 。

5.5 程序带宽

图 10 表明，当保持 $f_3$ 和 $V_D$ 不变时，若 Q_TC 小于 1.1，则 k_P下降，从而系统的稳态声功率额定值也下降。然而，从图 5 可明显看出，对于 Q_TC <1.1 ，最大振膜位移的频率 f_^xmax 低于 f₃ ，而且随着 Q_TC 的减小， f_^xmax 越来越远离 f₃ 。这表明对于播放能量在 f₃ 以下很少的节目内容时，系统的稳态额定值变得越来越保守。大多数放大器的功率带宽受限进一步降低了在 f_^xmax 频率下达到额定位移的可能性。
对于封闭箱体扬声器系统，用于高保真音乐再现且截止频率约为40 Hz或更低，或仅用于语音播放且截止频率约为 100 Hz或更低的情况，其程序功率额定值可近似认为是由公式(42)或图11给出的，在 Q_TC 不超过1.1的任何数值下均适用。当 Q_TC 超过该值时， f_^xmax 处于系统通带内，程序额定值实际上等同于稳态额定值。

5.6 电功率额定值

扬声器系统的位移限制电功率额定值与声功率额定值之间由系统参考效率相关联。因此，若已知系统的声功率额定值和参考效率，则相应的电功率额定值可通过两者的比值计算得出。
对于封闭箱体系统，公式 (24) 和 (39) 给出电功率额定值 为：

\[ P_{\text{ER(CB)}} = \pi \rho_0 c^2 \frac{f_c Q_{\text{EC}}}{V_{\text{AT}}} \cdot \frac{V_D^2}{|X(j\omega)|_{\text{max}}^2} ……(43) \]

将公式 (40) 除以 (26)，可以更清晰地看出该额定值与关键系统常数之间的关系：

\[ P_{\text{ER}} = \frac{k_P}{k_n} f_3 \frac{V_D^2}{V_B} ……(44) \]

特别需要认识到的是，对于给定的声功率容量，位移限制的电功率额定值与效率成反比。
对于大信号的位移非线性通常会使 P_ER 高于理论的线性值。因此，高输入功率额定值不一定是优点；它可能仅表明 k_η 值较小或允许的失真限较高。
制造商为扬声器系统指定的整体电功率额定值，必须考虑系统的位移限制功率容量 P_ER 、驱动单元的热限制功率容量 P_E(max) ，以及目标节目材料的频谱和统计特性。信号的统计特性对于判断是 P_ER 还是 P_E(max) 限制系统整体额定值至关重要，因为整体额定值设定了可安全使用的放大器的最大连续功率。为了保证可靠性和低失真，整体额定值绝不能超过 P_ER ；但可以根据目标节目材料的峰均功率比允许其超过 P_E(max) 。
选择扬声器系统以配合特定放大器（反之亦然）时，这一系统额定值非常关键。但必须记住，没有参考效率，电功率额定值无法说明声功率能力。

六、参数测量

已经证明，封闭箱体扬声器系统的重要小信号和大信号性能特征取决于少量基本参数。因此，测量这些基本参数的能力是一种非常有用的工具，不论是在评估现有扬声器系统性能时，还是在验证旨在满足特定性能标准的新系统设计时。

6.1 小信号参数：

\[ f_C , Q_{\text{MC}} , Q_{\text{EC}} , Q_{\text{TCO}}, a , V_{\text{AT}} \]

封闭箱体系统的音圈阻抗函数由公式 (22) 给出。该函数的稳态幅值  |Z_VC (j_ω )| 与归一化频率的关系如图 12 所示。

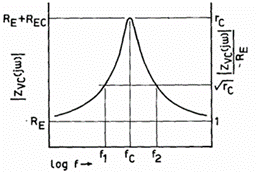
封闭箱系统的实测阻抗曲线与图12所示的形状非常接近。该阻抗曲线可以用于识别前四个参数，方法如下：
1) 测量直流音圈电阻 R_B ；
2) 找出阻抗幅值最大且相位为零（即阻抗为实数）时的频率 f_C ，将最大阻抗幅值与 R_E 的比值定义为r_c ；
3) 找出两个频率 f₁<f₂ 和 f₂>f_c ，使得阻抗幅值等于 R_B√( ^rc)；
4) 然后，结果如下所示：

\[ Q_{\text{MC}} = \frac{f_C \sqrt{r_O}}{f_2 – f_1} ……(45) \] \[ \] \[ Q_{\text{EC}} = \frac{Q_{\text{MC}}}{r_C – 1} ……(46) \] \[ \] \[ Q_{\text{TCO}} = \frac{Q_{\text{MC}}}{r_C} ……(47) \]

为了获得该系统的参数 a ，需将驱动单元从箱体中移出，并测量驱动单元参数 f_s，Q_MS 和 Q_ES （可以带或不带挡板），方法与上面系统的测量方法相同。顺应性比率可通过公式计算：

\[ a = \frac{f_C Q_{\text{EC}}}{f_S Q_{\text{ES}}} – 1 ……(48) \]

如果扬声器具有较大的音圈电感或系统存在较大的分频器电感，可能会导致阻抗幅值最大频率与相位为零的频率不一致。如果电感无法在测量时旁路或均衡，则最好将 f_c 定义为阻抗幅值最大的频率，而不考虑相位。但需注意，这种情况下的测量精度可能会有所下降。
V_AT 可由公式(1)、(11)、(15)、(25)和(34)计算得出：

\[ V_{\text{AT}} = \frac{V_{\text{AB}} V_{\text{AS}}}{V_{\text{AB}} + V_{\text{AS}}} = \frac{a}{a + 1} V_{\text{AB}} ……(49) \]

对于未填充材料的箱体，有 V_AB=V_B，此时可直接利用测得的 a 值计算 V_AT 。若系统箱体通常填充了吸音材料，则需要额外测量。
将填充材料从箱体中取出，或将驱动单元安装到一个类似但未填充的测试箱体中。对该组合测量其共振频率 f_CT 和对应的品质因数 Q_MCT，Q_ECT ，使用上述方法。然后，结果如下所示：

\[ V_{\text{AS}} = V_B \left( \frac{f_C T Q_{\text{ECT}}}{f_S Q_{\text{ES}}} – 1 \right) ……(50) \]

其中，V_B 是所用未填充箱体的净内部容积（可能是系统箱体或测试箱体）。根据公式(11)、(15)和 (34)，填充系统箱体的 V_AB 为：

\[ V_{\text{AB}} = \frac{V_{\text{AS}}}{a} ……(51) \]

该 V_AB 值可用于利用公式(49)计算 。

6.2 大信号参数：P_E(MAX) 和 V_D

扬声器的热功率容量测量最好交由制造商进行，他们熟悉所需技术，通常也愿意提供该信息。但通过音圈直径、长度、所用材料及扬声器预期用途，也可对热功率容量进行一定估算。
扬声器的位移体积 V_D 是有效振膜面积 S_D 与最大线性位移 x_max 的乘积。通常可通过估算振膜有效直径来求得 S_D 。部分制造商会提供扬声器的“冲程”（throw），通常为峰-峰值线性位移，即 2x_max 。若无此信息，可通过观察音圈超出磁隙的悬伸量估算 x_max 。若具备相应测试设备，可在空气中以正弦波输入扬声器共振频率，测量使得辐射声压总谐波失真达到约 10% 的峰值位移，从而更精确地评估该值。

七、箱体填充材料

在第4节中指出，向气悬式系统箱体中添加适当的填充材料会提升效率常数 。关于此类材料的使用和价值，已有大量争议和研究。
在高频（活塞工作范围及更高频率）内，填充材料用于抑制驻波的作用基本没有争议。争议集中在其在低频下的效果。更全面地了解这些材料的作用，有助于评估它们对不同用户的价值。

7.1 顺应性提升

如果所选填充材料具有低密度但高比热容，那么箱体内空气的压缩条件将从绝热过程转变为等温过程或部分等温过程 。这将增加箱体的有效声学顺应性（acoustic compliance），等效于增大了未填充箱体的容积。
顺应性理论上的最大提升可达 40%，但使用实际材料时，实际的提升通常不会超过约 25%。

7.2 质量加载（Mass Loading）

填充材料的添加通常会增加系统的总有效移动质量，这一点已由 Avedon 详细记录。其具体机制尚不完全明确，可能涉及填充材料本身的运动，或是振膜后部气流通道的收缩，从而对扬声器形成“质量加载”。这种质量增加的程度依赖于初始振膜质量和填充条件，可能从可忽略不计到高达 20%。

7.3 阻尼（Damping）

空气在填充的箱体中运动时会遇到摩擦阻力并损耗能量。因此，图1中的组件 R_ΔB 在箱体填充后会增加。系统总的机械损耗（R_AB+R_AS ）也因此增大，尤其是当填充材料较密、并且靠近扬声器（此处空气质点速度和位移最大）时更为明显。未填充系统的典型 Q_MC 值约为 5-10（主要来自扬声器悬挂系统的损耗），而填充系统通常具有 2-5 范围内的 Q_MC 值。

7.4 对设计师的价值（Value to the Designer）

当从零开始设计扬声器系统时，填充材料对顺应性的提升无疑是有利的。这意味着可以减小箱体尺寸、提高效率，或拓展频响。顺应性提升所伴随的质量增加可以在扬声器设计中加以补偿，使总移动质量达到期望值。填充材料引入的损耗在影响 k_n(Q) 方面是劣势，但为了由更高顺应性带来的 k_η 效率增益，这一代价是可以接受的。实际上，如果效率不是主要问题，那么摩擦损耗增加反而可适当放宽对磁路的要求，从而降低成本。
如果是围绕某个已选定扬声器来设计扬声器系统，填充材料所带来的顺应性增加依然是有利的，因为这允许在实现特定频响的前提下缩小箱体尺寸。质量增加会使扬声器参考效率按质量增幅的平方下降，这可能是期望的，也可能不是。同时，质量增加会在给定 f_c 情况下使 Q_EC 升高，而这一趋势又会被材料损耗对 Q_MC 的降低所抵消。
许多情况下，人们希望通过大量填充材料来补偿扬声器磁耦合不足造成的阻尼不足。只要填充材料对顺应性的提升大于对质量的增加，确实会略微降低 Q_EC 。尽管 Q_MC 可能大幅下降，但 Q_TC 的总下降通常不足以“拯救”一个严重欠阻尼的扬声器，中对此有说明。如果必须使用这样的扬声器，中描述的对扬声器本身进行声阻尼处理的方法比过度填充箱体更有效也更经济。

7.5 测量填充材料的效果（Measuring the Effects of Filling Materials）

填充材料对系统的具体影响可以通过对有/无材料情况下的系统参数进行仔细测量得出。Avedon使用的加重法在实验室条件下精度很高，但不适用于现场。可以采用第6节中描述的测量方法：

1. 将扬声器裸置在空气中或安装在测试挡板上，测量 f_s,Q_MS,Q_ES
2. 将扬声器安装到未填充的箱体中，测量 f_CT,Q_MCT,Q_ECT
3. 将扬声器安装到填充后的箱体中，测量 f_C,Q_MC,Q_EC
4. 总质量比（填充与未填充）为：

\[ \frac{M_{\text{AC}}}{M_{\text{ACT}}} = \frac{f_{\text{CT}} \cdot Q_{\text{EC}}}{f_C \cdot Q_{\text{ECT}}} ……(52) \]

由填充材料造成的箱体顺应性提升为：

\[ \frac{V_{\text{AB}}}{V_B} = \frac{ \left( \frac{f_{\text{CT}} \cdot Q_{\text{ECT}}}{f_S \cdot Q_{\text{ES}}} \right) – 1 }{ \left( \frac{f_C \cdot Q_{\text{EC}}}{f_S \cdot Q_{\text{ES}}} \right) – 1 }……(53) \]

5.材料对系统总阻尼的净效应可通过计算填充系统的 Q_TCO（用公式(9)或(47)）并与未填充系统的 Q_TCO=Q_MCTQ_ECT/(Q_MCT+Q_ECT) 进行对比。这些值代表每个系统在由近似零源阻抗的放大器驱动时的总 Q（即 Q_TC）。

通常结果是：填充材料同时增加顺应性和质量，但降低总 Q。其降低程度视材料的初始参数、选择以及在箱体中的放置位置而定。

下一篇