Biot 的孔隙弹性理论
在1956年,M. A. Biot 写了两篇文章 [Bio56a, Bio56b],提出了一种理论公式,用于描述饱和流体的各向同性多孔介质内的弹性波传播。这项工作的一个关键结果是存在三种波动:两种压缩波和一种剪切波。
已经有很多关于声学材料中 Biot 理论的书籍、论文或文章。本页面专注于一个基本观点和两个很少被讨论的轶事性评论。 为了为读者提供不同的“视角”,我们添加了一个可探索的解释和一个带有评论的 Matlab/GNU Octave 脚本。
最快的压缩波通常被称为P1波。最慢的压缩波通常被称为 P2 波。剪切波与各向同性弹性介质一样,被称为S波。
长波长(与孔隙尺寸相比)和小变形的假设确保在适用 Biot 理论时,流体性质(动态质量密度和动态体积模量)可以视为等同于当固体相不运动时的值。换句话说,孔隙骨架的变形对流体性质的影响不大。
Biot 的工作最初是为了地球物理学和石油勘探而开发的,在一段时间内引起了争议,原因有多个。
首先,由于导出波动方程所使用的技术:提出了一种形式的拉格朗日方法(在使用哈密尔顿原理之前)。事实上,均质化理论后来才得到发展。其次,Biot 工作的主要结果是预测出一种难以在低频(次声波)或高频(超声波)观察到的慢压缩波 P2,直到1980年 Plona 进行了超声实验证据 [Plo80],他观察到了与Biot 的预测一致的两种压缩波的传播时间,这一争议才解决。Plona 在水中观察了烧结玻璃珠的超声实验证据。
值得注意的是,声学家们在长时间以来,在测量多孔材料的平面波时,观察到了两种压缩波(虽然没有被识别为主要和次要压缩波)。例如,Leo Beranek 在1947年的发表物 [Ber47] 中的前两句话如下:“本文描述了对刚性声学瓷砖和软毯的研究。结果表明,两种波通过材料传播 – 一种主要是空气传播的波,另一种主要是结构传播的波”,在第564页中写到:“由于边缘的夹紧效应,可以清楚地看到材料的圆盘的谐振现象。”
以下应用程序允许您调整多孔材料的参数(建模为具有刚性骨架的 Biot-JCAL 或JCAL材料),并查看每个参数对该材料在刚性和不透水墙后的漫射吸声的影响。
JCAL曲线(■)是在考虑材料具有刚性且静止骨架的情况下获得的(即我们可以将该曲线视为仅P2波的结果)。考虑P1、P2和S波时,获得Biot-JCAL曲线(■)。Biot’s model | APMR (matelys.com)
Biot-JCAL 模拟是使用 [DBJ12] 引入的公式获得的(用于应用于双孔隙材料),并在 [BJ13] 中进一步详细说明并应用于多个模型(包括穿孔板)。用于计算这些漫射声场模拟的声学材料的传递矩阵方法(TMM),如 [JCAL 模型的 [BLA95] 和 Biot-JCAL 模型的 [DBGP13] 中实现的那样。
一种 TMM 的实现应该足够。这两个实现仅用于减少计算操作并在移动电话上提供几乎实时的体验。
这一部分的参考文献:
[Bio56a] M. A. Biot, Theory of propagation of elastic waves in a fluid saturated porous solid. I Low frequency range, J. Acoust. Soc. Am. 28, pp. 168–178, 1956.
[Bio56b] M. A. Biot, Theory of propagation of elastic waves in a fluid saturated porous solid. II Higher frequency range, J. Acoust. Soc. Am. 28, pp. 179–191, 1956.
[Plo80] T. J. Plona, Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies, Appl. Phys. Lett. 36, pp. 259-261, 1980.
[Ber47] L. L. Beranek, Acoustical Properties of Homogeneous, Isotropic Rigid Tiles and Flexible Blankets,J. Acoust. Soc. Am. 19(4), pp. 556-568, 1947.
[DBJ12] O. Dazel, F.-X. Bécot, L. Jaouen, Biot effects for sound absorbing double porosity materials, Acta Acustica United with Acustica 98(4), pp 567-576, 2012.
[BJ13] F.-X. Bécot, L. Jaouen, An alternative Biot’s formulation for dissipative porous media with skeleton deformation, J. Acoust. Soc. Am. 134 (6), pp. 4801-4807, 2013.
[BLA95] B. Brouard, L. Lafarge, J.-F. Allard, A general method of modelling sound propagation in layered media, J. Sound Vib. 183(1), pp. 129–142, 1995.
[DBGP13] O. Dazel, J.-P. Groby, B. Brouard, C. Potel, A stable method to model the acoustic response of multilayered structures, J. Appl. Phys. 113, 083506, 1995.
Matlab/GNU Octave script explained
BiotJCAL.m 是一个 Matlab/GNU Octave 脚本,用于计算使用 Biot 理论和 JCAL 模型对材料样品进行平面波正入射(因此无法与上面的漫射声场交互计算进行比较)的声吸收。为了检查脚本,我们将结果与来自传递矩阵方法(TMM)计算的结果之一(SolutionFromAlphaCell.rok)进行比较。两者的结果应该是等价的。
请记住,此脚本仅适用于平面波正入射。如果要获得漫射声场的声吸收,请尝试实施传递矩阵方法(TMM),而不是从此脚本开始。

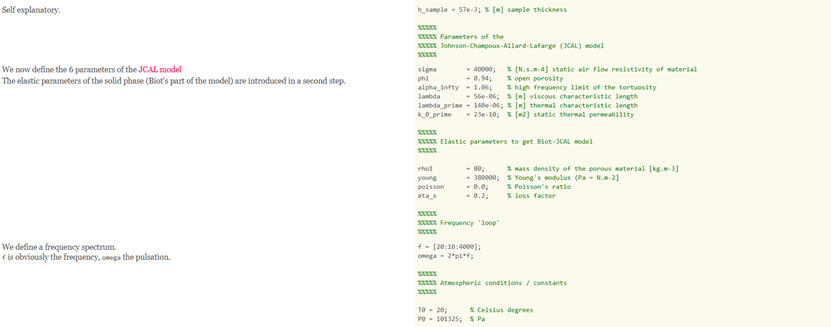


代码:
% Compute the sound absorption coefficient of a porous material sample
% for plane waves, at normal incidence (i.e. impedance tube conditions).
% The Biot-Johnson-Champoux-Allard-Lafarge (Biot-JCAL) model
% is used to compute the behavior of the material sample.
%
% No shear wave (S) is accounted here due to the conditions.
%
% This script is written using a e^{+j omega t} time convention.
%
% It’s not forbidden to keep the references reported in this work
% and to cite this work if you use it (there’s no shame to let others
% know you built nice stuff based on the works of other nice people).
%
% Copyleft 2012 luc.jaouen@matelys.com
% cf. APMR on the web:
% apmr.matelys.com/PropagationModels/BiotTheory/
% for more information.
clear all
close all
%%%%%
%%%%% Geometry
%%%%%
h_sample = 57e-3; % [m] sample thickness
%%%%%
%%%%% Parameters of the Johnson-Champoux-Allard-Lafarge (JCAL) model
%%%%%
sigma = 40000; % [N.s.m-4] static air flow resistivity of material
phi = 0.94; % open porosity
alpha_infty = 1.06; % high frequency limit of the tortuosity
lambda = 56e-06; % [m] viscous characteristic length
lambda_prime = 140e-06; % [m] thermal characteristic length
k_0_prime = 23e-10; % [m2] static thermal permeability
%%%%%
%%%%% Elastic parameters to get Biot-JCAL model
%%%%%
rho1 = 80; % mass density of the porous material [kg.m-3]
young = 380000; % Young’s modulus (Pa = N.m-2]
poisson = 0.0; % Poisson’s ratio
eta_s = 0.2; % loss factor
%%%%%
%%%%% Frequency ‘loop’
%%%%%
f = [20:10:4000];
omega = 2pif;
%%%%%
%%%%% Atmospheric conditions / constants
%%%%%
T0 = 20; % Celsius degrees
P0 = 101325; % Pa
%%%%%
%%%%% Do not modify anything below this line
%%%%% unless you understand what you’re doing
%%%%%
% Compute air parameters related to room conditions
% (acknowledgment goes to Dominic Pilon,
% dominic.pilon@metafoam.com, for gathering almost all these
% expressions from the references below)
%
% References:
% Lide, D. R. and Kehiaian H. V.,
% CRC. Handbook of Thermophysical and Thermochemical Data,
% CRC. Press Inc, 1994
%
% Touloukian, Y. S. and Makita, T.,
% Specific Heat – Non metallic Liquids and gases,
% The TPRC Data Series, Volume 6, IFI/PLENUM, 1970
%
% Pierce, A. D.,
% Acoustics, An Introduction to Its Physical Principles and Applications
% Acoustical Society of America, 2nd edition, 1989
% Convert temperature from Celsius to Kelvin
T = 273.16+T0;
% Universal gas constant (J.K-1.kg-1) [also 8.314 J.mol-1.K-1]
R = 287.031;
% Specific heat at constant pressure (J.kg-1.K-1; 260 K < T < 600 K
Cp = 4168.8(0.249679-7.55179e-5T+1.69194e-7T^2-6.46128e-11T^3);
% Specific heat at constant volume (J.kg-1.K-1; 260 K < T < 600 K
Cv = Cp-R;
% Dynamic viscosity (N.s.m-2; 100 K < T < 600 K
eta = 7.72488e-8T-5.95238e-11T^2+2.71368e-14*T^3;
% Ratio of specific heats
gamma = Cp/Cv;
% Density of air (kg.m-3)
rho0 = P0/(R*T);
% Velocity of sound (m.s^-1)
c0 = sqrt(gammaRT);
% Thermal conductivity (W.m-1.K-1) – cf A. D. Pierce p 513
kappa = 2.624e-02 * ( (T/300)^(3/2) * (300+245.4exp(-27.6/300))/(T+245.4exp(-27.6/T)) );
% Prandtl’s number
Pr = eta*Cp/kappa;
%%%%%
%%%%% COMPUTE THE DYNAMIC MASS DENSITY AND BULK MODULUS FOR THE MATERIAL
%%%%% JCAL MODEL
%%%%%
Gj = sqrt( 1 + 4jalpha_infty^2etarho0omega / … (sigma^2lambda^2*phi^2) );
rho_eq = (1/phi) * alpha_infty * rho0 * ( 1 + sigmaphiGj ./ …
(jomegarho0*alpha_infty) );
K_eq = (1/phi) * gammaP0 ./ … ( gamma – (gamma-1) ./ … ( 1 – jphikappa./(k_0_primeCpomegarho0) .* …
sqrt( 1+j4rho0omegaCpk_0_prime^2/(kappalambda_prime^2*phi^2) ) ) );
K_e = K_eq*phi;
%%%%%
%%%%% COMPUTE EQUIVALENT MASS DENSITIES AND BIOT PARAMETERS
%%%%%
% Using the formalism introduced in
% O. Dazel, F.-X. Becot, L. Jaouen,
% Biot effects for sound absorbing double porosity materials,
% Acta Acustica United with Acustica 98(4), pp 567-576, 2012.
% and further detailed in
% F.-X. Becot, L. Jaouen,
% An alternative Biot’s formulation for dissipative porous media with skeleton deformation,
% J. Acoust. Soc. Am. 134 (6), pp. 4801-4807, 2013.
%
% Equation numbers correspond to those from
% – J.-F. Allard, Propagation of sound in porous media, first ed., 1993
% – or second ed., 2009, with N. Atalla
rho_22_tilde = rho_eqphi^2; rho_11_tilde = rho_eqphi^2-phirho0+rho1; rho_12_tilde = phirho0-rho_eq*phi^2;
N = (young(1+ieta_s))/(2(1+poisson)); KB = (2/3)N(1+poisson)/(1-2poisson); % eq. 6.29
rho_s_tilde = rho_11_tilde-((rho_12_tilde.^2)./rho_22_tilde);
P_tilde = (((1-phi)^2)/phi).K_e+KB+(4/3)N; % eq. 6.28
Q_tilde = (1-phi)K_e; % eq. 6.27 R_tilde = phiK_e; % eq. 6.26
%%%%%
%%%%% COMPUTE COMPLEX WAVE NUMBERS
%%%%%
delta = (((P_tilde.rho_22_tilde)+(R_tilde.rho_11_tilde)-(2.Q_tilde.rho_12_tilde)).^2) … % eq. 6.71
-(4.(P_tilde.R_tilde-Q_tilde.^2).(rho_11_tilde.rho_22_tilde-rho_12_tilde.^2));
sdelta = (sqrt(delta));
% Take square root of delta having a positive real part
if real(sdelta) < 0
sdelta = – sdelta;
end
delta_1 = sqrt((omega.^2./(2.(P_tilde.R_tilde-Q_tilde.^2)))… % eq. 6.69
.(P_tilde.rho_22_tilde+R_tilde.rho_11_tilde-2.Q_tilde.*rho_12_tilde+(sdelta)));
delta_2 = sqrt((omega.^2./(2.(P_tilde.R_tilde-Q_tilde.^2)))… % eq. 6.70
.(P_tilde.rho_22_tilde+R_tilde.rho_11_tilde-2.Q_tilde.*rho_12_tilde-(sdelta)));
mu_1 = ((P_tilde.delta_1.^2)-(rho_11_tilde.omega.^2))./((rho_12_tilde.omega.^2)-(Q_tilde.delta_1.^2)); % eq. 6.73
mu_2 = ((P_tilde.delta_2.^2)-(rho_11_tilde.omega.^2))./((rho_12_tilde.omega.^2)-(Q_tilde.delta_2.^2)); % eq. 6.73
%%%%%
%%%%% CHARACTERISTIC IMPEDANCES OF WAVES FOR SOLID AND FLUID PHASES
%%%%%
Z1f = (R_tilde+Q_tilde./mu_1).delta_1./(phiomega); % eq. 6.75
Z2f = (R_tilde+Q_tilde./mu_2).delta_2./(phiomega); % eq. 6.76
Z1s = (P_tilde+Q_tilde.mu_1).delta_1./omega; % eq. 6.78
Z2s = (P_tilde+Q_tilde.mu_2).delta_2./omega; % eq. 6.79
%%%%
%%%%% COMPUTATION OF THE SURFACE IMPEDANCE
%%%%%
D = (1-phi+phimu_2).(Z1s-(1-phi).Z1f.mu_1).tan(delta_2h_sample) + …
(1-phi+phimu_1).(Z2f.mu_2.(1-phi)-Z2s).tan(delta_1h_sample); % eq. 6.109
Zs = -1j(Z1s.Z2f.mu_2-Z2s.Z1f.mu_1)./D; % eq. 6.108 %%%%% %%%%% COMPUTE SOUND ABSORPTION COEFFICIENT %%%%% alpha = 1 – ( abs( (Zs-rho0c0)./(Zs+rho0*c0) ) ).^2;
alphacell = load(‘SolutionFromAlphaCell.rok’);
%%%%%
%%%%% PLOT THE RESULT
%%%%%
figure(1)
set(gca,’FontSize’,16)
hold on
plot(f,alpha,’r-‘,’Linewidth’,2)
plot(alphacell(:,1),alphacell(:,2),’y–‘,’Linewidth’,2)
xlabel(‘Frequency (Hz)’)
title(‘Normal sound incidence (Biot-JCAL model)’)
set(gca,’Ylim’,[0 1])
