直接辐射式扬声器系统分析

本文翻译自 RICHARD H. SMALL 的 Direct-Radiator Loudspeaker System Analysis*一文

引言

在许多有关扬声器的讨论中充斥着模糊不清的术语，这种混乱的根源很可能正是该领域术语本身的不统一。“扬声器”一词早已失去了其具体含义。尽管各国曾尝试将其定义为仅指驱动单元或仅指完整系统，该词至今仅在通用意义或作为形容词时仍具价值。为了澄清起见，本文采用以下更具体的常用术语。
声源（Source）：一种设备，通常为电子功率放大器，用来以规定的电压或功率水平提供电能。
扬声器驱动单元（Loudspeaker driver）：一种将电能转换为机械能和（或）声能的换能器结构。本文讨论最常见的一种——动圈式驱动单元，其由位于永久磁化气隙中的音圈与连接悬挂振膜（或“锥盆”）的结构组成。
挡板（Baffle）：一种支撑驱动单元并减少或防止来自振膜正面与背面相位相反的声波相互抵消的结构。
箱体（Enclosure）：用于安装驱动单元并辐射声音的箱体或箱壳。箱体形成一个封闭的几何表面，仅在驱动单元处安装孔或其他指定孔处开口。
扬声器系统（Loudspeaker system）：驱动单元（或多个驱动单元）与号角、挡板或箱体等结构性辐射辅助装置的组合，用于将规定声源的电能转换为声能。
直辐射式扬声器系统（Direct‑radiator loudspeaker system）：将声能直接从驱动单元振膜和（或）简单箱体孔口耦合到空气中，而不使用号角或其他声阻抗匹配装置的扬声器系统。
活塞范围（Piston range）：指驱动单元振膜周长小于声波波长的频率范围。在此频率范围内，使用驱动单元安装于箱体中的直辐射系统具有基本无指向性的声输出。

扬声器系统设计

直辐射式扬声器系统已有约半个世纪的使用历史。在此期间，人们对各类直辐射系统的行为特性积累了大量知识，但仍不均衡且不完备。例如，封闭箱体系统的理解远胜于通气箱系统，而有关被动辐射器系统的定量设计信息在公开文献中几乎找不到。
传统上，扬声器系统的设计是一种基于经验的试错过程：先选定一款可能合适的驱动单元，再不断调整箱体设计，直至系统性能令人满意。与之鲜明对比的是其他许多工程系统的综合设计方法——从所需性能规格出发，直接推导出系统组件的规格。
后一种方法要求工程师精确掌握系统性能与组件参数之间的关系。本文所述分析方法是获得这一知识的手段，针对所有类型直辐射扬声器系统的低频性能；该方法基于此类系统的高通滤波特性。

扬声器系统灵敏度与效率

理想的麦克风能以相同灵敏度将声压转换为电压。录制与重放系统的设计旨在无失真地处理代表声压的信号电压。要完成声音重放过程，理想的扬声器系统应以相同灵敏度将电压转换为声压。
实际上，所有扬声器系统都具有有限带宽。在低频区，它们表现为高通滤波器。因此，扬声器系统的低频设计可视为高通滤波器的设计。主要区别在于扬声器系统设计师对“电路”配置的控制非常有限；其设计自由度仅限于通过调整系统组件值以获得最佳性能。
电滤波器的频率响应通常以无量纲的电压或功率比描述。由于扬声器系统是换能器，其灵敏度随频率的响应为声压与电压的比值。然⽽，也可定义为与上述灵敏度比的平方成正比的无量纲功率比。
在系统辐射无指向性的频率范围内，自由场中固定距离处的声压与系统辐射的声功率平方根成正比。源在固定阻抗上输⼊的电功率与源输出电压的平方成正比。因此，系统实际声输出功率与同一声源在固定阻抗上输⼊的电功率之比，恰好等于系统灵敏度比（即系统频率响应）的平方（仅差常数因子）。若选定的固定阻抗能较好地代表扬声器系统的输入阻抗，则系统通带内该功率比值即为系统的额定电声转换效率。
此定义扬声器效率的方法在原理上与 Beranek 所使用的“可用功率效率”定义相似，因为两者都能揭示系统的精确频率响应。本文方法的主要优点在于：计算所得的系统通带效率与声源输出阻抗无关，且能真实地将系统声输出能力与声源的电功率额定值联系起来。

小信号性能关系

声学输出功率

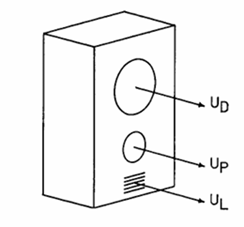
图1示意了一般化直辐射扬声器系统。箱体设有驱动单元、导向管（或被动辐射器）及泄漏口的孔口。对驱动单元施加电激励后，在振膜、导向管和泄漏口产生体积速度，分别记为 U_D ,U_P ,U_L 。
在极低频时，箱体各孔口尺寸和间距远小于波长，此时系统可视为若干重合简单声源的组合。其声输出等效于单一简单源，强度 U₀ 为各孔口体积速度的矢量和：

\[ U_0 = U_D + U_P + U_L······(1) \]

系统辐射的声功率为：

\[ P_A=|U_0 |^2 R_{AR} ······(2) \]

其中
P_A：声输出功率
R_AR：系统的辐射负载阻性部分
式 (2) 在驱动单元活塞范围的上限内通常都成立，因为在高于该频率范围时，驱动单元往往是唯一显著的辐射源。
Allison 和 Berkovitz 最近的研究表明，在典型聆听室内，扬声器系统低频负载本质上等同于无限挡板上一侧活塞的负载。该辐射负载的阻性部分为[^3]：

\[ R_{AR} = \frac{\rho_0 \omega^2}{2\pi c} ······(3) \]

其中
ρ₀：空气密度
ω：稳态角频率
c：声速
式 (3) 仅在活塞范围内有效，但在此范围内 R_AR 与箱体尺寸及孔口无关。

由于质量无法在音箱边界处产生或储存，并且由于声压通常远小于大气压，因此质量守恒要求：

\[ U_0=-U_B ······(4) \]

其中 U_B 是进入音箱的总体积流速。即使音箱在内部被划分为多个部分，公式（4）也仍然成立。如果音箱包含多个腔体，则有：

\[ U_B=U_{B1}+U_{B2}+U_{B3}+⋯, ······(5) \]

式（5）右侧的每一项表示进入各个独立腔体的净体积流速。
公式（1）、（4）和（5）是通用的，适用于任意数量的腔体和开口以及它们的任意互联结构。它们是矢量方程，要求考虑各个分量之间的相对相位关系。
尽管公式（4）非常简单，但在分析使用音箱的直射式扬声器系统时，它具有关键意义。结合公式（2）来看，它揭示了系统所辐射的声功率与压缩和扩展音箱内空气的体积流速直接相关。Beranek、de Boer以及其他研究者在分析低音反射式音箱时已指出这一点；而这一结论同样适用于所有的直射式系统音箱。

电输入功率

这里所定义的扬声器系统的名义电输入功率是：源施加于一个等于扬声器音圈电阻的电阻上所传递的功率。因此：

\[ P_E = \left[\frac{e_g}{R_g + R_E}\right]^2 R_E ······(6) \]

其中：
P_E：名义电输入功率
e_g：电源的开路输出电压
R_g：电源的输出电阻
R_E：驱动器音圈的直流电阻
R_E 的值通常约为标称驱动器音圈阻抗的 80%。
美国、英国和国际标准在计算扬声器驱动器的名义输入功率时，使用了各种定义的额定阻抗。由于系统计算的声输出功率依赖于 R_E，而非人为设定的额定阻抗，本定义简化了下文推导的理论系统效率表达式。在将计算得到的活塞频段参考效率与依照上述标准测得的效率进行比较时，必须记住这一差异。

效率

由公式（2）和（6）可得，扬声器系统的名义功率传输比或效率 η 为：

\[ \eta = \frac{P_A}{P_E} = \frac{|U_0|^2 R_{AR} (R_g + R_E)^2}{e_g^2 R_E} ······(7) \]

要对给定系统评估该效率表达式，需要知道 U₀ 与 e_g 之间的关系。这个关系可以通过分析系统的声学等效电路来获得。
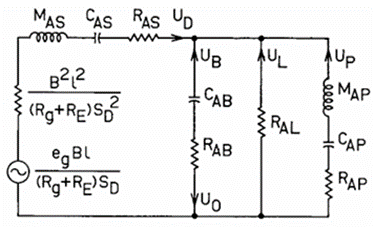
Olson 和 Beranek 对声学等效电路的推导做了非常详尽的描述。图 2 是图 1 中通用扬声器系统的阻抗类型声学等效电路。在图 2 中，
B：驱动器气隙中的磁通密度
l：在气隙磁场中音圈导体的长度
S_D：驱动器振膜的有效投影面积
M_AS：包括音圈及空气负载在内的驱动器振膜组件声质量
C_AS：驱动器悬挂系统的声顺应度
R_AS：驱动器悬挂系统损耗的声阻尼
C_AB：箱体内空气的声顺应度
R_AB：箱体内部能量吸收造成的声阻尼
R_AL：箱体泄漏造成的声阻尼
M_AP：包括空气负载在内的导向孔（或无源辐射器）的声质量
C_AP：导向孔（或无源辐射器）悬挂系统的声顺应度
R_AP：导向孔（或无源辐射器）损耗的声阻尼
从图 2 的电路出发，可以通过移除或短接合适的元件，得到大多数常见直射式系统的声学等效电路。请注意，在该类等效电路中，电压代表声压，电流代表体积流速。

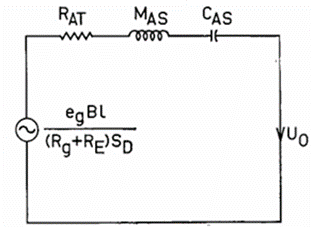
无限障板扬声器系统的声学等效电路是从图 2 的通用电路中推导而来的，通过移除代表被动辐射器和音箱漏泄的支路，并将代表音箱内部的支路短接，使得音箱耗散为零、顺应为无穷，从而得到图 3 所示的电路。
在该电路中，通过将剩余的串联电阻组合，得到了总的声阻：

\[ R_{AT} = R_{AS} + \frac{B^2 l^2}{(R_g + R_E) S_D^2} ······(8) \]

根据图 3 的电路分析可得：

\[ U_0 = \frac{e_g B l}{(R_g + R_E) S_D s M_{AS}} \cdot G(s) ······(9) \]

其中：

其中，s 是复频率变量。
在稳态正弦激励下，s=jω，将公式（5）和（9）与公式（7）结合，可以得出无限障板系统的效率表达式：

\[ \eta(j\omega) = \frac{\rho_0}{2\pi c} \cdot \frac{B^2 l^2}{R_E S_D^2 M_{AS}^2} \cdot |G(j\omega)|^2 ······(11) \]

其中 G(jω) 是公式（10）中 G(s) 在 s=jω 情况下的表达。
需要注意的是，G(jω) 包含了公式（11）中所有与频率相关的项；其余部分仅包含物理量、数值常数和扬声器驱动器的常量。
公式（11）中的最后一部分，也就是 |G(jω)|²，是无限障板系统的频率响应，表现为归一化功率比。因此，声压与信号源电压的归一化比值，即归一化灵敏度或声压频率响应，就是|G(jω)|；从公式（10）可知，它是一个二阶（每倍频程 12dB 衰减）的高通滤波函数。
对于任何使用音箱的直射式扬声器系统，其总体积流速和效率的表达形式与公式（9）和（11）相同；唯一的区别是每种系统的 G(s) 函数不同。
系统响应函数 G(s) 包含了系统的幅频响应、相频响应和瞬态响应的全部信息。G(s) 总是一个高通滤波函数，其在通带中的值为 1。因此，公式（11）中不含频率的常数部分即为系统的通带效率。

假设与近似

声学等效电路（图 2 和 3）仅在驱动单元的活塞范围内有效；各电路元件在该频率范围内的数值假定与频率无关。
对分析无显著影响、阻抗较小的电路元件将被忽略。其中之一是辐射阻抗；虽然它负责声音辐射功率并已包含在式(2)中，但其数值远小于声学电路中的其他阻抗，且随频率平方变化，故在简化分析时可忽略。此外，驱动单元音圈的电感在本分析的有限频带内影响也可忽略。
声学质量元件的处理简化为将等效电路同一支路上串联出现的所有质量相加，即物理质量与空气负载质量合并。合并后总质量对频率基本恒定，但在实际系统中，驱动单元的安装位置或条件可能影响其等效质量，测量与使用时需注意这一点。

小信号参数

系统的响应函数及相关方程通常包含驱动单元、箱体和声源参数。要将这些关系用于实际设计，必须已知或可测量各参数值。
识别与测量系统参数的关键在于构建系统的电气等效电路。该电路是声学等效电路的对偶形式，可参照文献 [H. F. Olson, Dynamical Analogies (Van Nostrand, NewYork,1943)] 及 [L. L. Beranek, Acoustics (McGraw-Hill, York, 1954).,ch. 3] 推导而来。通过分析电气等效电路，即可得到实际系统音圈端口阻抗与物理组件之间的对应关系，从而通过阻抗测量确定系统参数。

驱动单元参数

驱动单元小信号性能的基本电机参数包括 R_E, (B l), S_D, C_MS, M_MS 和 R_MS，其中：

• C_MS：驱动单元悬挂机构的机械顺应度（=C_AS/S_D²）
• M_MS：驱动单元振膜组件（含音圈及空气负载）的机械质量（=M_AS/S_D²）
• R_MS：驱动单元悬挂机构的机械损耗阻力（=R_AS S_D²）

这些参数互相独立，可分别调整，并各自影响系统的小信号响应。
为便于设计与测量，常用 Thiele 所定义的四个基本参数代替上述参数，它们与上述量相关且更易测定：

• f_s：驱动单元运动系统的谐振频率（式 (12) 定义），通常以无挡板状态（f_SA）或指定挡板状态（f_SB）给出
• V_AS：驱动单元的声学顺应度，换算成等效空气体积（式(15)）
• Q_MS：在 f_s 处，驱动单元电气等效摩擦阻力与反射运动性抗抗的比率（式定义），相当于 Thiele 的 Q_a
• Q_ES：在 f_s 处，音圈直流电阻与反射运动性抗抗的比率（式(14)定义），相当于 Thiele 的 Q_c

参数 Q_MS 和 Q_ES 对应于 Thiele 的 Q_a 和 Q_e。它们末尾加上了额外的下标 S，以明确它们仅适用于驱动器本身，并防止与系统参数 Q_M 和 Q_E（对应 Thiele的 Q_a 和 Q_b（总体））混淆——这些系统参数在本节末尾定义。

驱动单元电气等效电路

图 4 给出了驱动单元（在空气中或安装于无限挡板上）的电气等效电路，其对偶于声学电路（图 3）。电路元件对应关系为：

C_MES：驱动单元机械质量对应的电气电容（=M_ASS_D²/(B l)²）
L_CES：驱动单元机械顺应度对应的电气电感（=C_AS (B l)²/S_D²）
R_ES：驱动单元机械损耗对应的电气电阻（=(B l)²/(S_D²R_AS )）
驱动单元谐振频率 ω_S=2πf_s 的特征时间常数 T_S

\[ \begin{aligned} T_S^2 &= \frac{1}{\omega_S^2}\\ & = C_{MES} L_{CES} \\ &= C_{AS} M_{AS} \end{aligned} ······(12) \]

若仅考虑 R_ES，驱动单元谐振电路的品质因数为

\[ \begin{aligned} Q_{MS} &= \omega_S C_{MES} R_{ES} \\ &= \frac{1}{\omega_S C_{AS} R_{AS}} \end{aligned} ······(13) \]

若仅考虑 R_E（即 R_g=0），则

\[ \begin{aligned} Q_{ES} &= \omega_S C_{MES} R_E\\ & = \frac{\omega_S R_E M_{AS} S_D^2}{(B l)^2} \end{aligned} ······(14) \]

驱动单元在空气中的等效顺应度体积为

\[ V_{AS} = \rho_0 c^2 C_{AS} ······(15) \]

驱动单元音圈阻抗函数

图 4 中音圈端右侧电路的等效阻抗为

\[ Z_{VC}(s) = R_E + R_{LS} \left[ \frac{\frac{s T_S}{Q_{MS}}}{s^2 T_S^2 + \frac{s T_S}{Q_{MS}} + 1} \right] ······(16) \]

将 s=jω 后，其幅值曲线（图 5）呈现一个由 R_E 向上平移的谐振峰。

驱动单元参数测量

将驱动单元置于空气中或简易测量挡板上，绘制其音圈阻抗随频率变化曲线，可得到与图 5 相同形状的曲线。谐振频率 f_s 处阻抗最大，定义最大阻抗与直流电阻 R_E 之比为 r₀。在阻抗为√(r₀ ) R_E的两侧频率
f₁<f_s 与 f₂>f_s 处，可由下式计算：

\[ Q_{MS} = \frac{f_s \sqrt{r_0}}{f_2 – f_1}, \quad Q_{ES} = \frac{Q_{MS}}{r_0 – 1} ······(17) \]

为测量 V_AS，将驱动单元安装于一个已知净容积 V_T 的无衬里小测量箱中，重新测得新谐振频率 f_CT 和电气品质因数 Q_ECT。
则

\[ V_{AS} = V_T \left( \frac{f_{CT} Q_{ECT}}{f_s Q_{ES}} – 1 \right) ······(18) \]

声源参数

影响扬声器系统小信号性能的功放参数包括频率响应和输出电阻。
频率响应：优质功放的带宽和幅度平坦度通常超出扬声器系统本身，故系统效率表达式中的频率响应即可有效描述从功放输入端到声输出的整体低频响应。如需，可在功放端加装电滤波器以修正响应。
输出电阻 R_g：与音圈直流电阻 R_E 串联，共同决定驱动支路的总品质因数。现代功放多设计为高阻尼因子，即 R_g 远小于预期的 R_E，这一条件常假设成立，并据此调整驱动单元参数以获得所需总 Q。若功放与扬声器系统作为一体设计，可通过反馈技术将等效源电阻调为正、零或负，从而获得更多设计自由度。

功放源电阻测量

用正弦信号驱动功放，分别在空载和额定负载条件下测量输出电压：空载时为e₀，负载时为e_L，负载电阻为R_L。则功放等效输出电阻为：

\[ R_g = R_L \frac{e_0 – e_L}{e_L} ······(20) \]

如果 e₀ 和 e_l ,之间没有可测量的差异，那么就其对总 Q 的影响而言，可以认为 R_g 为零。在这种情况下，不需要精确测量，因为重要的是总电阻 (R_g+R_R )。
放大器规格通常给出在 1kHz 频率下测得的 R_g 值（或针对额定负载的阻尼因子）。但在计算低频下系统 Q 时，50Hz下测得的数值更有意义。

放大器源电阻的测量

可以通过向放大器输入一个正弦信号，并在无负载和额定负载条件下测量放大器的输出电压来确定 R_g 的值。如果无负载输出电压为 e₀，负载输出电压为 eL，负载电阻为 R_L，则有：

\[ R_g = R_L \frac{e_0 – e_L}{e_L} ······(20) \]

如果 e₀ 和 e_L 之间没有可测量的差异，就其对总 Q 的影响而言，可以认为 R_g 为零。在这种情况下，不需要精确测量，因为重要的是总电阻 (R_g+R_R )。
放大器的规格通常给出在 1kHz 下测得的 Rg 值（或额定负载下的阻尼因子）。但在计算低频下的系统 Q 时，在 50Hz 下测得的值更有意义。

箱体参数

箱体参数的数量取决于系统的类型。参考图 2，图中右侧所有的垂直支路都包含箱体元件。
箱体最重要的性质是其物理体积 V₁，它决定了顺应性 C_AB。如果系统中包含元件 M_A（不论是否包含 C_AP），箱体将表现出一个共振频率 f_B（或时间常数 T_B）。如果存在 C_AP，则会引入额外的共振频率 f_P（或时间常数 T_P）。箱体或开口的损耗可以通过在指定频率（ f_B 或 f_P ）下定义各支路的 Q 值来进行表征。

箱体参数的测量

通常，当驱动单元被安装在箱体中时，其音圈阻抗会发生变化，通过这种变化可以识别出箱体参数。由于每种类型的箱体系统对应的关系不同，因此此处不作具体说明，将在后续介绍各类系统的论文中详细给出。

复合系统参数

在直辐射扬声器系统的分析中，某些元件参数的组合在描述系统的函数中自然而一致地出现。其中之一是驱动单元顺应性与箱体顺应性的比值 C_AS/C_AB。这个参数，即系统顺应性比，是使用箱体的直辐射系统中的一个基本参数。它出现在 Beranek 和 Thiele 的分析中，以及 Novak 使用的等效刚度比形式 S_B/S_S 中。由于该参数对系统性能具有重要意义，因此给予它一个简化符号；在后续的论文中，将使用 Benson 引入的符号a。
在调谐箱体系统中，频率比 f_B/f_S 自然地出现在分析中。这被称为系统调谐比；Novak 将其记为符号 h。
在每一种类型的系统中，驱动单元参数 Q_ES 都会因源电阻 R_g 的存在而改变，形成一个系统参数：

\[ Q_E = Q_{ES} \frac{R_g + R_E}{R_E} ······(21) \]

(R_g+R_E ) 的有效值包括连接导线和分频器电感中的任何显著电阻。
类似地，如果系统的声学类比电路在 R_As 串联有一个声阻抗元件，则驱动单元的 Q_MS 参数也会发生变化。新的系统参数 Q_M 通常通过测量得出。
系统中驱动单元支路的总 Q 由以下复合系统参数给出：

\[ Q_T = \frac{Q_E Q_M}{Q_E + Q_M} ······(22) \]

频率响应

响应函数

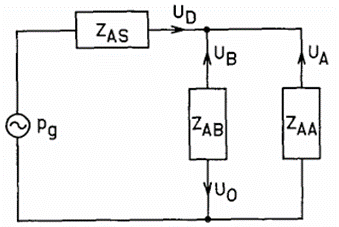
扬声器系统的响应函数 G(s) 可以从先前所示的完整效率表达式中获得，也可以通过一种更简单的一般方法得出，仅提供响应函数本身。如图 6 所示，将图 2 中的声学类比电路简化为四个基本元件：
p_g：声学驱动压力，表示为：

\[ p_g = \frac{e_g B l}{(R_g + R_E) S_D} ······(23) \]

Z_As：驱动单元支路的阻抗，通常表示为：

\[ Z_{AS}(s) = R_{AT} + s M_{AS} + \frac{1}{s C_{AS}} ······(24) \]

Z_AB：表示箱体内部的支路阻抗，通常表示为：

\[ Z_{AB}(s) = R_{AB} + \frac{1}{s C_{AB}} ······(25) \]

Z_AA：所有除驱动单元外的箱体开口所对应的阻抗，这些开口共同贡献于输出的总体容积速度。注意图 6 中的 U_A 等于图 2 中的 U_L 与 U_P 之和。Z_AA 由具体的箱体设计决定。
响应函数在所有情况下均为：

\[ \begin{aligned} G(s) &= \frac{s M_{AS} U_0}{p_g} \\ &= \frac{s M_{AS}}{Z_{AB} + Z_{AS} + \frac{Z_{AB} Z_{AS}}{Z_{AA}}} \end{aligned} ······(26) \]

响应函数的简化

从系统声学类比电路获得的响应函数始终是一个归一化的高通滤波器函数，其形式为 s 的两个多项式的比值。多项式系数中包含了系统中各种声质量、顺应性和阻尼的组合。
如果将这些系数中的声学量替换为前一节所述的简化系统参数，则响应函数更易于理解。由于这些系数必须具有时间的维度，因此始终可以将它们重新定义为系统的时间常数（或共振频率），再辅以如 Q 值、顺应性比、质量比和电阻比等无量纲参数。这些变量对于电气工程师而言比抽象的声学量更容易理解。
对于前面分析的无限障板系统，响应函数 G(s) 如式 (10) 所示。通过以下替换可以简化表达式：

\[ T_S^2 = C_{AS} M_{AS} ······12 \]

以及：

\[ Q_T = \frac{1}{ω_S C_{AS} R_{AT}} ······(27) \]

其中 Q_T 是连接到声源的驱动单元在频率 f_S 处的总 Q 值，这与式 (22) 中定义的参数一致。于是得到：

\[ G(s) = \frac{s^2 T_S^2}{s^2 T_S^2 + \frac{s T_S}{Q_T} + 1} ······(28) \]

使用响应函数

一旦已知系统的响应函数，只要系统参数是已知或可测的，就可以确定任何特定设计系统的响应。这一过程有助于判断现有或拟议系统的响应表现，但对于如何改进此类系统则帮助有限。
更有用的方法是研究系统响应函数的行为，判断哪些系数（即参数值）能产生最理想的响应特性。这听起来像是一个适合用计算机执行的复杂而耗时的任务，但幸运的是，滤波器设计者已对扬声器系统设计中最常关注的响应形式（如通带平坦响应）进行了深入研究。
由于扬声器系统在低频下具有最小相位特性，其幅度、相位、延迟和瞬态响应彼此关联，无法独立指定。音频系统中最常见的最优响应标准是最大带宽内的幅度响应平坦性，但在某些情况下，设计者可能更关注瞬态响应或延迟特性。无论使用何种设计标准，其本质都是转化为一组最优多项式系数，以便据此指定或调整系统参数。
调整扬声器系统响应的过程显然类似于传统滤波器类型的对准。这种相似性在目标是达到预定响应状态而非反复试错优化时尤为明显。
再次考虑无限障板系统，其响应函数由式 (28) 给出。滤波器设计者通常使用的这一类响应函数的通用形式为：

\[ G(s) = \frac{s^2 T_0^2}{s^2 T_0^2 + a_1 s T_0 + 1} ······(29) \]

其中：

• T₀：标称滤波器时间常数
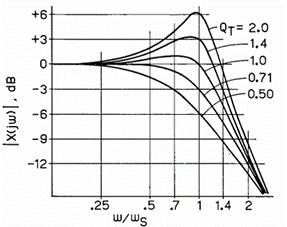
• a₁：阻尼或响应形状系数 式(29)的行为已广为人知，因此当 T_S=T₀ 且 Q_T=1/a₁时，就可以推断无限障板系统的响应行为。使用式 (29) 的标准曲线，图 7 中绘制了多个 Q_T 值下的稳态幅度响应|G(jω)|。
• Q_T=0.50 的曲线对应谐振电路的临界阻尼条件；
• Q_T=0.71 的曲线为最大平坦（Butterworth）对准，幅度无峰值；
• Q_T=1.0、1.4、2.0 的曲线分别具有约 1dB、√3dB 和 6dB 的幅度峰值，但相比最大平坦对准，半功率带宽有所扩展。
• 对于这个简单系统，设计工程师可以选择所需的响应形状，并据此指定系统参数，同时还能直观地看出参数公差带来的影响。

参考效率

扬声器系统效率表达式 (11) 的前半部分只包含物理常数和驱动单元参数，而最后一部分，即系统响应函数的平方，在系统截止频率以上的活塞工作范围内始终为1。因此，该表达式的前半部分就是系统的通带效率或“参考效率”，记为 η₀，其表达式为：

\[ η_0 = \frac{ρ_0}{2πc} \cdot \frac{B^2 l^2}{R_E S_D^2 M_{AS}^2} ······(30) \]

按照电-机械驱动单元的基本参数，表达式也可以写成：

\[ η_0 = \frac{ρ_0}{2πc} \cdot \frac{B^2 l^2}{R_E} \cdot \frac{S_D^2}{M_{MS}^2} ······(31) \]

需要注意的是，M_AS 和 M_MS 都包括相关的空气负载质量以及系统施加的任何人为质量加载。 将式 (12)、(14)、(15) 与式 (30) 结合，可以得到参考效率的新表达式：

\[ η_0 = \frac{4π^2}{c^3} \cdot \frac{f_s^3 V_{AS}}{Q_{ES}} ······(32) \]

这表明参考效率可以完全通过基本的驱动单元参数来计算，这些参数在“小信号参数”章节中已有讨论。这个结果看起来令人惊讶，因为这些参数仅通过简单的电学测量就能获得。这意味着无需任何机械、磁性或声学测量就可以得出系统在活塞范围内的电声效率。
需要指出的是，式 (32) 的效率值比 Thiele 的表达式大一倍，这是因为 Thiele 的表达式是针对 4π 球面自由场的辐射负载推导的，而式 (32) 采用的是 2π 球面自由场辐射负载，这在典型听音室中更接近实际的扬声器系统辐射条件。
式 (32) 中的物理常数在国际单位制下的值为 9.6×10^-7。当 f_s 以赫兹为单位，V_AS以立方米为单位时，可用以下形式计算效率： 若 V_AS 以升（liters）为单位（1升=10^-3立方米）：

\[ η_0 = 9.6 \times 10^{-10} \cdot \frac{f_s^3 V_{AS}}{Q_{ES}} ······(33) \]

若 V_AS 以立方英尺（cubic feet）为单位：

\[ η_0 = 2.7 \times 10^{-8} \cdot \frac{f_s^3 V_{AS}}{Q_{ES}} ······(34) \]

计算出的效率值可以转换为分贝形式 (10log₁₀ η₀ ) 或百分比形式 (100η₀ )。直射辐射式系统（direct-radiator systems）的参考效率通常非常低，大约只有1%左右。
扬声器驱动单元的共振频率通常在其安装于面积为数平方米的标准测试障板上时测量。也有制造商使用等效无限障板或完全无障板。由于大多数驱动单元最终都将安装在箱体中，因此系统设计者更关注在模拟箱体空气负载质量条件下的共振频率、Q 值和参考效率；此条件最接近于有限的“标准”障板。
如果系统对驱动单元进行了有意的质量加载（如在其前方安装受限孔径），则系统的参考效率会低于驱动单元的基本效率。但只要 f_s 和 Q_ES 的测量是在质量加载条件下进行的，仍然可以使用式 (32) 计算系统效率。根据式 (30) ，效率的降低与质量增加的平方成正比。

大信号性能

功率额定值与大信号参数

扬声器标准仅为建立扬声器（驱动单元）功率额定值提供了一个大致的指导：输入功率的额定值应使得具有相同无失真输出功率额定值的功放可以与扬声器配合使用而不会造成损坏或产生过度失真。
在中高频段，由于驱动单元的振膜位移要求较小，扬声器系统的功率承载能力主要受到驱动单元音圈散热能力的限制。这种限制导致了一个热限制的绝对最大输入功率额定值，无论系统设计如何，该功率值由驱动单元本身决定，记作 P_E(max) 。
在低频段，驱动单元需要产生更大的振膜位移，因此需要确定一个输入功率额定值，以确保振膜不会超过指定的位移极限。这种受位移限制的输入功率额定值通常低于 P_E(max) 。由于振膜位移取决于箱体设计，这种位移限制的功率额定值是系统的特性，而不是驱动单元本身的，但它仍依赖于驱动单元的最大位移能力。
对于特定驱动单元，其位移极限可以基于多种标准确定，其中包括：

1. 防止悬挂系统损坏；
2. 限制频率调制失真；
3. 限制非线性失真（如谐波失真和调幅失真）。

在本文讨论范围内，假设可以定义一个峰值位移极限，记为 x_max 。
那么，在低频下驱动单元的基本大信号参数为：

\[ V_D = S_D \cdot x_{\text{max}} ······(35) \]

其中 V_D 表示最大容许的位移体积（Displacement Volume），S_D 是振膜的有效面积，x_max 是峰值位移极限。

该参数，即振膜峰值位移体积（Diaphragm Peak Displacement Volume），表示驱动器振膜从静止到达到最大位移极限时所排开的空气体积。它描述了位移体积的限制，因此也描述了驱动器的体积速度与频率之间的限制关系。该参数的实际用途将在下节说明。
因此，除了前面讨论的小信号参数之外，系统设计者还必须了解（或规定）大信号参数 P_E(max) 和 V_D。

振膜位移

扬声器系统驱动单元的小信号振膜位移可以通过系统声学等效电路来确定。首先分析电路得到振膜的体积速度 U_D，再除以有效面积 S_D 得到振膜速度 u_D，再除以 s（即积分）得到振膜位移 x_D。该位移表达式通常具有以下形式：

\[ x_D = P_E^{1/2} σ_x(P) k_x X(s) ······(36) \]

其中： P_E：标称输入功率，定义见公式 (6)
σ_x(P) ：未封装驱动器的静态（直流）位移灵敏度，单位为米/瓦^1/2，表达式为：

\[ \begin{aligned} σ_x(P) &= \left[\frac{C_{MS}^2 B^2 l^2}{R_E}\right]^{1/2} \\ &= \left[\frac{V_{AS}}{2πρ_0 c^2 f_s Q_{ES} S_D^2}\right]^{1/2} \end{aligned} ······(37) \]

k_x：系统位移常数，不大于1
X(s)：归一化系统位移函数，为低通滤波器函数，s=0 时值为1 对于特定系统，k_x X(s) 可以通过两种方法之一计算得到：

1. 如上述方式建立表达式(36)，再除以 P_E^1/2 σ_x(P) ，结合公式 (6) 和 (37)。
2. 分析声学等效电路中信号源所见导纳，并除以 sC_AS，参考图6，有：

\[ k_x X(s) = \frac{1}{s C_{AS}} \cdot \frac{1 + \frac{Z_{AB}}{Z_{AA}}}{Z_{AB} + Z_{AS} + \frac{Z_{AB} Z_{AS}}{Z_{AA}}} ······(38) \]

结果可拆解为常数因子 k_x 和在零频率处归一化为 1 的频率依赖因子 X(s)。 对于无限障板系统，图 3 电路分析表明位移常数为 1，位移函数为：

\[ X(s) = \frac{1}{s^2 T_S^2 + \frac{s T_S}{Q_T} + 1} ······(39) \]

该函数的稳态幅值|X(jω)|随归一化频率的变化曲线绘于图 8 中。对于该简单系统，其曲线是图7中响应曲线的镜像。

位移限制下的功率额定值

电功率额定值

假设驱动器在大信号输入下振膜位移呈线性，并将x_D的峰值限制为x_max，则可得扬声器系统在正弦稳态条件下受位移限制的电功率额定值：

\[P_{ER} = \frac{1}{2} \left[\frac{x_{\text{max}}}{σ_x(P) k_x |X(jω)|_{\text{max}}}\right]^2 ······(40) \]

P_ER：位移限制下的电输入功率额定值，单位为瓦 |X(jω)|_max：系统位移函数的最大幅值，即振膜位移最大的频率处的值 将公式 (35) 与 (37) 代入公式 (40)，可得：

\[ P_{ER} = πρ_0 c^2 \cdot \frac{f_s Q_{ES} V_D^2}{V_{AS} k_x^2 |X(jω)|_{\text{max}}^2} ······(41) \]

声功率额定值

扬声器系统的位移限制电功率额定值对可使用的放大器连续输出功率构成限制。该功率额定值与系统的参考效率一起决定了系统通带上平坦部分可辐射的最大连续声功率。因此，使用公式(32)和(41)，扬声器系统的稳态位移限制声功率额定值 P_AR 为：

\[ P_{AR} = \frac{4π^3 ρ_0}{c} \cdot \frac{f_S^4 V_D^2}{k_x^2 |X(jω)|_{\text{max}}^2} ······(41) \]

该额定值可以轻松转换为标准辐射与测量条件下的声压级额定值，例如参见 [International Recommendation, Electrotechnical Commission, “IEC Methods of Measurement for Loud speakers,” IEC Publ. 200 (1966).] 第 3.16 节。对于 SI 单位，即 f_s 以 Hz 表示，V_D 以 m³ 表示，因子 4π³ρ₀/c 的数值为 0.42。

无限障板系统的功率额定值

将 k_x=1 代入公式 (42) 中的 k_x，可以得到安装在无限障板上的驱动器的位移限制声功率额定值：

\[ P_{AR(IB)} = \frac{4π^3 ρ_0}{c} \cdot \frac{f_S^4 V_D^2}{|X(jω)|_{\text{max}}^2} ······(43) \]

对于给定的 V_D 值，声功率额定值对驱动器谐振频率有较强的依赖性。同时，它也会受到 Q_T 的影响（通过|X(jω)|”max” ，见图 8），当 Q_T≤0.71 时该额定值达到最大。
例如，考虑一个无限障板系统，其谐振频率为 50Hz，具有二阶巴特沃斯响应。如果驱动器为一个 12 英寸单元（有效半径为 0.12m），并具备 ±4mm 的峰值位移能力，那么 V_D=0.18dm³，由此得出的声功率额定值为 P_AR=0.086 瓦。这相当于在 1 米距离下的声压级为 101.5dB。
将公式 (41) 中的 k_x 设为单位 1，可得该无限障板系统的位移限制电功率额定值为：

\[ P_{ER(IB)} = πρ_0 c^2 \cdot \frac{f_S Q_{ES} V_D^2}{V_{AS} |X(jω)|_{\text{max}}^2} \]

这个公式定量地说明了一个公知事实：为声悬挂系统设计的低谐振频率、高顺应性低音扬声器（woofer），如果用于空气中或无限障板上，其输入功率处理能力会远低于传统低音扬声器。
在上述数值示例中，系统的电功率额定值取决于驱动器的顺应性。如果驱动器的总移动质量为 30 克，根据公式(12)，驱动器的顺应性应为 V_AS=0.1m³。忽略机械损耗并取 Q_ES=Q_T=0.71，则根据公式(44)，电功率额定值为 P_ER=5瓦。比较 P_AR 和 P_ER 或使用公式(33)，驱动器的参考效率为 η₀=1.7%。
注意，相同的额定值也适用于一个使用 8 英寸驱动器（有效半径为 0.08m）、最大位移能力为 ±9mm（使得 V_D=0.18dm³）、谐振频率、声顺应性及 Q 值与上述相同的无限障板系统。

假设与修正

所计算的位移限制功率额定值的准确性取决于两个假设：

1. 振膜位移在达到 x_max 前是线性的；
2. 信号源的功率带宽一直延伸到最大位移对应的频率。

这两个假设可能会导致保守的功率估算。
例如，上述的无限障板系统在非常低的频率下才达到最大位移。而该系统通常由低频截止为 30Hz(-3dB) 的放大器驱动。如果将 Q_T=0.71 情况下的|X(jω)|（恒压驱动）曲线乘以该放大器的归一化功率输出曲线，得到的|X(jω)|最大值会从 1 降至约 0.7。因此，一个更实际的功率额定值为 P_ER=10 瓦，P_AR=0.17瓦。
同样，如果 x_max 被定义为超出驱动器线性范围的位移，那么实际达到该峰值位移所需的输入功率会比计算值更高。可通过驱动器的实际“输入功率 vs. 位移”特性曲线轻松计算修正因子。

结论

直接辐射式扬声器系统的低频响应、效率和功率额定值由系统部件的参数决定。这些关系是互为反向的：系统性能的设定会对组件参数提出明确要求。系统中最重要的部件是驱动器，只有在规定了足够数量的小信号和大信号参数时，驱动器的性能才能被完整描述。
本文分析的一个有趣结果是：驱动器振膜面积 S_D 并未显式出现在扬声器系统的小信号响应、小信号效率或位移限制功率额定值公式中。这意味着理论上可以设计出不同直径但具有相同 f_S , Q_MS , Q_ES , V_AS , V_D 参数的驱动器。如果安装在相同的箱体中，这些驱动器将具有相同的小信号性能和位移限制功率能力。主要区别在于，较大的驱动器成本更高，但所需振膜位移更小，因此在相同声输出下产生的调制失真更小。
尽管电动的动圈驱动器在全球范围已被生产数十年，但几乎没有制造商提供其产品的完整低频参数，也很少有人提出相关要求。未来，基于目标性能规格的系统合成将日益取代使用现成驱动器的试错式设计方法。这将要求驱动器制造商能够满足此类参数需求，并随产品提供完整的参数信息。
本文中用于描述驱动器行为的参数集并非唯一的，但它们易于测量、易于理解，并且（如后续文章将显示）非常适用于整个系统的分析与设计。

附录：驱动器参数测量

驱动器的 Q 值

根据公式(13)和(14)，

\[ \frac{Q_{MS}}{Q_{ES}} = \frac{R_{ES}}{R_E} ······(45) \]

由图 5 可知，音圈最大阻抗与直流电阻之比为：

\[ \begin{aligned} r_0 &= \frac{R_{ES} + R_E}{R_E} \\ &= 1 + \frac{Q_{MS}}{Q_{ES}} \end{aligned} ······(46) \]

因此可得：

\[ Q_{ES} = \frac{Q_{MS}}{r_{0} – 1} ······(18) \]

另外，当信号源阻抗为零（R_g=0）时，驱动器的总品质因数 Q_TS 为：

\[ \begin{aligned} Q_{TS} &= \frac{Q_{MS} Q_{ES}}{Q_{MS} + Q_{ES}} \\ &= \frac{Q_{MS}}{r_0} \end{aligned} ······(47) \]

由此，公式 (16) 可写成：

\[ Z_{VC}(s) = R_E \cdot \frac{r_0 + Q_{MS} \left(s T_S + \frac{1}{s T_S}\right)} {1 + Q_{MS} \left(s T_S + \frac{1}{s T_S}\right)} ······(48) \]

其幅值平方为：

\[ |Z_{VC}(jω)|^2 = \frac{R_E^2 \left[r_0^2 + Q_{MS}^2 \left(\frac{ω}{ω_S} – \frac{ω_S}{ω}\right)^2\right]} {1 + Q_{MS}^2 \left(\frac{ω}{ω_S} – \frac{ω_S}{ω}\right)^2} ······(49) \]

在任意两个频率 ω₁<ω₂ 且满足 ω₁ ω₂=ω_S² 的条件下，根据公式 (49) 可得阻抗幅值相等。设该幅值为：

\[ |Z_{VC}(jω_{1})| =|Z_{VC}(jω_{2})|= r_1 R_E ······(50) \]

则：

\[ \begin{aligned} |Z_{VC}(jω_{1,2})|^2 &= r_1^2 R_E^2 \\ &= \frac{R_E^2 \left[r_0^2 + Q_{MS}^2 \left(\frac{ω_2-ω_1}{ω_S}\right)^2\right]} {1 + Q_{MS}^2 \left(\frac{ω_2-ω_1}{ω_S}\right)^2} \end{aligned} ······(51) \]

从中可推导出：

\[ Q_{MS} = \frac{ω_S}{ω_2 – ω_1} \cdot \sqrt{\frac{r_0^2 – r_1^2}{r_1^2 – 1}} ······(52) \]

当 r₁=√(r₀) 时，上式简化为：

\[ Q_{MS} = \frac{f_s \sqrt{r_0}}{f_2 – f_1} ······(17) \]

选择 r₁=√(r₀) 不仅使计算变得简单，而且能提高测量精度，因为此时 f₁ 和 f₂ 之间间隔较大，且位于阻抗曲线斜率较高的区域。
如上所述，当音圈阻抗幅值等于 √(r₀ ) R_E 时所对应的频率 f₁ 和 f₂ 应满足如下条件：

\[ \sqrt{(f_1 f_2 )}=f_s ······(53) \]

对于大多数实际驱动器而言，这一关系并不完全成立，因为驱动器的基本参数（尤其是顺应性和机械阻尼）会随频率或振膜位移而略有变化。如果音圈电感较大，也会对阻抗曲线产生偏移。然而，对于大多数设计良好的驱动器，利用公式 (53) 得到的结果与实际测量值的误差一般在 1Hz 以内。因此，公式 (53) 是一种非常有用的校验手段，可用于识别测量误差或识别不能用一组常值参数准确建模的驱动器。

驱动器顺应性

一个简单的未衬垫的测试外壳在大气压力下具有一个声学顺应性 C_AB，它与其净内腔体积 V__T 之间的关系为：

\[ C_{AB} = \frac{V_T}{\rho_0 c^2} ······(54) \]

一个具有总声学质量 M_AS 和顺应性 C_AS 的驱动器，其自谐振频率定义为：

\[ T_S^2 = \frac{1}{\omega_S^2} = M_{AS} C_{AS} ······(12) \]

当该驱动器安装在封闭的测试箱中时，将测得一个新的谐振频率，表示为：

\[\begin{aligned} T_{CT}^2 &= \frac{1}{\omega_{CT}^2} \\ &= M_{ACT} \frac{C_{AB} C_{AS}}{C_{AB} + C_{AS}} \end{aligned} ······(55) \]

其中 M_ACT 是由于振膜空气负载质量的变化而导致的新总运动质量。然后：

\[ \frac{\omega_{CT}^2}{\omega_S^2} = \frac{M_{AS}}{M_{ACT}} \left[1 + \frac{C_{AS}}{C_{AB}}\right] ······(56) \]

根据公式(14)：

\[ Q_{ES} = \frac{\omega_S R_E M_{AS} S_D^2}{B^2 l^2} ······(57) \]

类似地，

\[ Q_{ECT} = \frac{\omega_{CT} R_E M_{ACT} S_{D^2}^2}{B^2 l^2} ······(58) \]

因此，

\[ \frac{M_{AS}}{M_{ACT}} = \frac{\omega_{CT} Q_{ES}}{\omega_S Q_{ECT}} ······(50) \]

结合公式 (56) 和 (59)，得到：

\[ 1 + \frac{C_{AS}}{C_{AB}} = \frac{\omega_{CT} Q_{ECT}}{\omega_S Q_{ES}} ······(60) \]

从公式 (15) 和 (54) 中，得到：

\[ \frac{C_{AS}}{C_{AB}} = \frac{V_{AS}}{V_T} ······(61) \]

因此，

\[ \frac{V_{AS}}{V_T} = \frac{\omega_{CT} Q_{ECT}}{\omega_S Q_{ES}} – 1 ······(62) \]

或

\[ V_{AS} = V_T \left[\frac{f_{CT} Q_{ECT}}{f_S Q_{ES}} – 1\right] ······(63) \]

初始的驱动器测量（ f_S 和 Q_ES）可以在任何大小的反射板上进行，或者没有反射板。然而，特别是对于低共振驱动器，建议将驱动器的轴线保持水平，以避免由于重力导致过大的静态振膜位移。
测试外壳墙壁的能量吸收仅影响测量值 Q_MCT，因此不会影响顺应性计算。然而，放置在外壳内的吸声材料可能会影响 C_AB 的值，因此不应使用。
特别需要避免测试外壳的泄漏，因为泄漏也会改变 C_AB 的有效值，从而严重影响测量的准确性。测试外壳必须仔细构造，并且必须检查驱动器的安装垫圈是否紧密密封。一些驱动器具有内置的泄漏路径，可能通过音圈周围或多孔的边缘悬浮材料泄漏。对这些驱动器的测量结果必须谨慎使用。要检测泄漏，可以在大约 10Hz 的输入信号下应用适中的信号电平，并仔细听所有周围区域的“呼吸”声，这通常是泄漏的迹象。

测量技术

我特别感谢 A. N. Thiele 提出了基于滤波器的分析方法和本论文中描述的简单参数测量方法，并感谢 J. E. Benson 提出了简单的广义扬声器系统概念，为术语和符号的讨论贡献了大量时间，并仔细检查了手稿中的方程式和计算。
扬声器阻抗测量通常采用恒压驱动或恒流驱动方法。如果驱动器完全线性或测量电平足够低，两个方法应得出相同的结果。恒压法的优点在于其更接近驱动器通常的工作条件。
准确测量小信号参数需要信号电平足够小，以便所有的电压和电流波形保持不失真正弦波。使用示波器观察波形，并相应调整信号电平。尤其是对于高顺应性、未负载的驱动器，通常需要在 0.1 瓦特或更低的输入电平下进行测量。
使用直流桥准确测量驱动器音圈电阻。然后，可以制作与此电阻值相同的假负载，并用作测量阻抗的设备校准负载。
不要相信音频扫频型节拍频率振荡器的频率刻度。为了最大限度地提高准确性，应使用频率计数器或稳定且经过准确校准的正弦波发生器的刻度进行频率读数。

致谢

本文是关于直射辐射电动扬声器系统低频性能研究项目的结果之一。我感谢悉尼大学电气工程学院为提供研究设施、监督和帮助，并感谢澳大利亚联邦教育与科学部的财政支持。
许多作者通过他们的公开作品为本文中所发展的基本思想做出了贡献。