从时域到自适应分解：一文读懂滚动轴承早期故障诊断

1.1 滚动轴承的重要性及故障危害

滚动轴承作为一种标准化的、不可或缺的机械基础件，在国民经济的各个领域中扮演着至关重要的角色。从日常生活中的家用电器到高端制造领域的精密机床、航空航天发动机，再到风力发电机、高速列车等大型装备，滚动轴承都以其高效的承载能力、较低的摩擦阻力以及便捷的互换性，广泛应用于支撑旋转部件、引导运动、传递载荷和保证运转精度等方面，被誉为“工业的关节”。据统计，旋转机械的故障中，有相当一部分是由滚动轴承失效引起的，其故障率在某些行业甚至高达 30% – 40%。

然而，滚动轴承的工作环境往往十分复杂和苛刻，例如高速、重载、高温、腐蚀性介质以及长时间连续运转等。这些因素，加之轴承自身结构特点（如滚动体与滚道的反复接触应力、载荷分布不均）以及制造、安装和润滑方面可能存在的问题，使得滚动轴承成为机械设备中最易损坏的薄弱环节之一。常见的故障模式包括内外圈的剥落、裂纹、点蚀，滚动体的磨损、压痕，以及保持架的断裂等。这些故障一旦发生，初期可能表现为设备振动和噪声的轻微增大，若未能及时发现和处理，故障会迅速扩展，导致设备性能急剧下降、停机时间延长、维修成本增加，甚至引发灾难性的安全事故，造成巨大的经济损失和人员伤亡。

1.2 早期故障检测的意义与挑战

传统的设备维护方式主要依赖于定期维修或故障后维修。定期维修往往基于经验或统计数据，可能导致维修不足（故障提前发生）或过度维修（浪费资源和时间）。故障后维修则更为被动，不仅维修成本高昂，而且可能造成严重的生产中断和安全隐患。随着工业4.0和智能制造的推进，基于状态的维护（Condition Based Maintenance, CBM）和预测性维护（Predictive and Health Management, PHM）的理念日益受到重视。这些先进的维护策略核心在于实时监测设备运行状态，在故障发生的早期阶段甚至萌芽阶段进行准确诊断和预警，从而为制定科学的维护计划、优化备件库存、延长设备使用寿命、提高设备可靠性和安全性提供关键支持。

滚动轴承的早期故障通常指故障的初始阶段，此时故障特征非常微弱，产生的异常信号很容易被设备运行过程中的强背景噪声、其他部件的振动以及复杂传递路径的影响所淹没。这给早期故障的准确检测带来了巨大挑战。因此，研究和开发高灵敏度、高可靠性的滚动轴承早期故障检测技术，对于提升现代工业设备的智能化运维水平具有重大的理论价值和广阔的应用前景。

1.3 基于振动信号的监测方法概述

滚动轴承的故障会引发多种物理现象的变化，如温度升高、润滑油中出现磨粒、声发射信号以及振动信号的改变等。尽管温度监测、油液分析、声发射监测等技术在特定场合有其应用价值，但基于振动信号的监测与诊断技术因其信息丰富、易于获取、非侵入式以及对早期故障相对敏感等优点，已成为目前应用最为广泛且研究最为深入的方法。当滚动轴承内部出现局部缺陷（如点蚀、裂纹）时，滚动体每次滚过缺陷处都会产生一次或多次冲击脉冲，这些脉冲会激起轴承系统及其周围结构的固有频率振动，形成具有调制特性的振动信号。通过分析这些振动信号的特征变化，可以有效地检测和诊断轴承的早期故障。

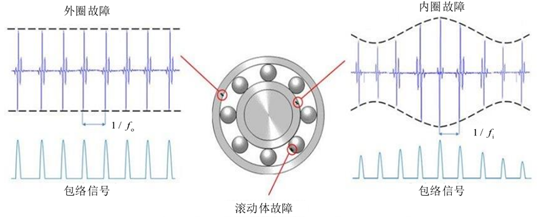
1.3.1 基于振动信号的早期故障特征提取技术

从混有强噪声的振动信号中提取微弱的早期故障特征是诊断成功的关键。常用的振动信号处理与特征提取技术包括时域分析、频域分析、时频域分析以及更高级的自适应信号分解方法。

（1）时域分析

时域分析直接对振动信号的时间波形进行统计分析，计算简单，反映信号的整体能量和冲击特性。常用的时域统计参数包括：

均方根值 (Root Mean Square, RMS)：反映信号的平均能量。

\[ F_{rms}(t) = \sqrt{\frac{1}{N} \sum_{n = 1}^{N} [F(t, n)]^2} \]

其中 F(t,n) 是时刻 t 的第 n 个采样点幅值，N 是采样点数。

峰值 (Peak)：信号幅值的最大绝对值。

\[ F_p(t) = \max \{ |F(t, 1)|, |F(t, 2)|, \ldots, |F(t, N)| \} \]

峭度 (Kurtosis)：衡量信号波形中冲击成分的尖锐程度，对早期冲击性故障敏感。

\[ F_{kurt}(\hat{t}) = \frac{\frac{1}{N} \sum_{n = 1}^{N} [F(t, n) – F_{mean}(\hat{t})]^4}{[F_{std}(\hat{t})]^4} = \frac{1}{N [F_{std}(\hat{t})]^4} \sum_{n = 1}^{N} [F(t, n) – F_{mean}(\hat{t})]^4 \]

峰值因子 (Crest Factor)：峰值与均方根值的比值，反映冲击的相对强度。

\[ F_{crest}(t) = \frac{F_p(t)}{F_{rms}(t)} \]

时域参数对故障敏感性不一，且易受噪声和工况波动影响，对于早期微弱故障的识别能力有限。

（2）频域分析

频域分析技术通过将时域振动信号转换至频率域，旨在揭示信号中隐含的周期性成分，特别是与轴承特定故障模式相关的特征频率。这种转换通常借助于傅里叶变换实现，其分析结果能够为故障诊断提供直接的频率特征依据。

频谱分析：对原始振动信号或其预处理后的信号应用傅里叶变换，可以得到信号的幅值谱或功率谱。在这些谱图中，可以直接观察是否存在由轴承故障引起的特征频率及其谐波分量。对于周期平稳信号，频谱分析能够清晰地展现各频率成分的能量分布。

包络分析 (Envelope Analysis)：包络解调分析是诊断滚动轴承（尤其是处于早期故障阶段）故障的一种核心且高效的频域技术。其物理基础在于，当轴承存在局部缺陷时，滚动体周期性地冲击缺陷处，会产生一系列重复性的瞬态冲击响应。包络解调的目的正是从这种高频调制信号中提取出低频的故障特征信息。标准的包络解调分析流程通常包含以下关键步骤：

解析信号构建：对原始振动信号 x(t) 应用希尔伯特变换 (Hilbert Transform) H{x(t)}，构建其对应的解析信号 z(t)：

\[ z(t) = x(t) + j\mathcal{H}\{x(t)\} \]

包络提取：计算解析信号 z(t) 的瞬时幅值，即为其包络信号 Ex(t)：

\[ E_x(t) = |z(t)| = \sqrt{x^2(t) + (\mathcal{H}\{x(t)\})^2} \]

包络谱计算：对提取得到的包络信号 Ex(t) 进行傅里叶变换，得到包络谱 ESx(f)：

\[ ES_x(f) = \mathcal{F}\{E_x(t)\} \]

尽管频域分析方法，特别是包络解调，在滚动轴承故障诊断中具有重要地位，但对于由早期微弱故障引起的、信噪比极低的非平稳信号，故障特征在频域（包括包络谱）中仍可能模糊不清或被噪声干扰。

（3）时频域分析

由于滚动轴承早期故障产生的振动信号往往具有非平稳特性，传统的时域或频域分析方法在揭示这类信号的深层特征时存在局限性。时频域分析方法能够同时提供信号在时间和频率上的局部信息，更适合处理非平稳、时变的振动信号。

短时傅里叶变换 (Short-Time Fourier Transform, STFT)：STFT 是最早也是最直观的时频分析方法之一。其核心思想是采用一个固定长度的分析窗函数 w(t) 对信号 x(t) 进行分段截取，并假定在每个窗口内信号近似为平稳的，然后对每个窗内的信号段进行傅里叶变换，从而得到信号的局部频谱。

\[ STFT_x(\tau, f) = \int_{-\infty}^{\infty} x(t) w(t – \tau) e^{-j 2 \pi f t} dt \]

其中，τ 表示时间窗的中心位置，f 表示频率。

Wigner-Ville 分布 (WVD)：WVD 是一种经典的二次型时频分布，对于单分量线性调频信号可以提供理想的时频能量聚集性。其定义为信号瞬时自相关函数的傅里叶变换：

\[ WVD_x(t, f) = \int_{-\infty}^{\infty} x\left(t + \frac{\tau}{2}\right) x^*\left(t – \frac{\tau}{2}\right) e^{-j 2 \pi f \tau} d\tau \]

（4）时频高级自适应信号分解技术

为克服传统时频分析方法中基函数选择困难、时频分辨率受限或交叉项干扰等问题，研究者们开发了一系列数据驱动的自适应信号分解技术。这些方法能够根据信号自身的内在特性将其分解为一系列更简单、更具物理意义的子分量（模态），从而便于后续的故障特征提取和分析。

经验模态分解 (Empirical Mode Decomposition, EMD)：

EMD 是由 Huang 等人提出的一种强大的自适应时频分析方法，特别适用于处理非线性和非平稳信号。EMD 的核心思想是将任何复杂信号 x(t) 分解为有限数量的、具有良好时频局部性的本征模态函数 imf₁(t) 和一个单调的残余分量 r_L(t)。分解过程基于信号的局部特征时间尺度，通过一个“筛选”(sifting)过程迭代提取IMFs。每个 IMF 代表信号在不同时间尺度上的振荡模式。

\[ x(t) = \sum_{l = 1}^{L} \text{imf}_l(t) + r_L(t) \]

奇异值分解 (Singular Value Decomposition, SVD)：

SVD 是一种强大的矩阵分解技术，能够揭示数据的主要能量分布和结构特性，常用于信号去噪和特征提取。对于一维振动信号 x(t)，通常先通过相空间重构或构建Hankel矩阵将其转换为一个矩阵形式，然后进行 SVD，具体如下：

①Hankel 矩阵构建：将信号段重构成一个 m×(N−m+1) 的 Hankel 矩阵。采用了一种特定的 2×(N−1) 矩阵构建方式：

\[ H = \begin{pmatrix} x_1 & x_2 & \cdots & x_{N – 1} \\ x_2 & x_3 & \cdots & x_N \end{pmatrix} \]

②对矩阵 H 进行 SVD 分解：

\[ H = U S V^T = \sum_{k = 1}^{\min(2, N – 1)} \sigma_k u_k v_k^T \]

其中，U=[u₁,u₂] 和 V=[v₁,v₂….,v_N-1] 为正交矩阵，S 是一个对角线上元素为奇异值 σ_k (σ₁≥σ₂≥…≥0) 的对角矩阵。较大的奇异值通常对应信号的主要能量成分（近似信号），较小的奇异值对应噪声或细节信息（细节信号）。通过对奇异值进行选择性重构，可以实现信号的去噪或分解。

总而言之，滚动轴承的早期故障诊断是一个持续发展的领域，从传统的时域、频域分析到先进的时频分析和自适应分解技术，信号处理方法不断演进，以期更精准、更可靠地捕捉故障的蛛丝马迹。未来，结合多种信号处理技术的优势，并融入人工智能与机器学习算法，将是实现滚动轴承智能化健康管理的关键趋势。